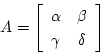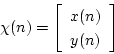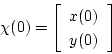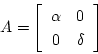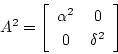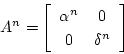: 行列の対角化
: Dsys
: Dsys
狼とウサギがある地域に生きている様を想像しましょう.ウサギは,草を食べ,
子孫を増やし,狼はそのウサギ゛を食べ,やはり自分の子孫を増やしていきます.
今の世代の個体数は,その前の親の世代の個体数に依存します.
狼が増えすぎて,ウサギを食べ過ぎて少なくなったら,狼も食料が少なくなって
狼も数が減ります.逆に,狼が少なくなりすぎて,ウサギが増えすぎたら,草が食べ
尽くされてウサギの餌がなくなりウサギが減少,それに伴って狼もというようにです.
実際の自然界では,人間と言う「外乱」が邪魔をしない限り,それぞれの生き物達が
絶妙のバランスを保って生きています.生態系を表すモデル式の詳しい話しは別の
機会として,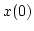 と
と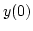 で今のウサギと狼の個体数,
で今のウサギと狼の個体数, 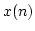 と
と 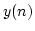 で,
で, 年後のそれぞれの個体数を表すとすれば,ウサギと狼の個体数の変化を表す式は
年後のそれぞれの個体数を表すとすれば,ウサギと狼の個体数の変化を表す式は
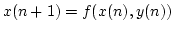 |
|
|
(1) |
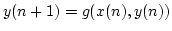 |
|
|
(2) |
という式で表されるでしょう.この式の意味するところは,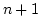 年後の
ウサギと狼の個体数がその前の年のウサギと狼の個体数
年後の
ウサギと狼の個体数がその前の年のウサギと狼の個体数 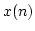 と
と 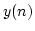 で決まる
事を表しています.
狼とウサギが生きている環境は毎年同じ(気象の変動や,人間の環境破壊など
外乱は無いもの)としています.
で決まる
事を表しています.
狼とウサギが生きている環境は毎年同じ(気象の変動や,人間の環境破壊など
外乱は無いもの)としています. 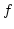 や
や 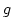 がどんな関数を表すかは取り合えず置いて
おきますが,このような方程式は,生態系に限らず,物理系,機械系,社会経済,
etcにも現れます.(無論,計算機関係にも)
今後,このような式を扱って行くわけですが,先ずは最も簡単なものから手を付けます.
がどんな関数を表すかは取り合えず置いて
おきますが,このような方程式は,生態系に限らず,物理系,機械系,社会経済,
etcにも現れます.(無論,計算機関係にも)
今後,このような式を扱って行くわけですが,先ずは最も簡単なものから手を付けます.
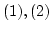 式の替わりに
式の替わりに
を扱います.
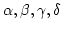 は定数とします.
行列とベクトルを使えば,
は定数とします.
行列とベクトルを使えば,
として
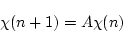 |
(3) |
と表すことができます.
から始めて
 式から
式から
でさらに
続けると
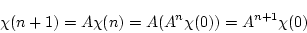 |
(4) |
となります.
まずは手始めに,
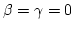 という特別な場合を考えましょう.
という特別な場合を考えましょう.
ですから
さて以下の練習問題を解いてください.
練習問題 1
- [(0)]
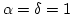 のとき
のとき
- [(1)]
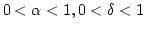 のとき
のとき
- [(2)]
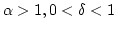 のとき
のとき
- [(3)]
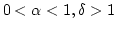 のとき
のとき
- [(4)]
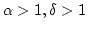 のとき
のとき
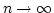 とすると
とすると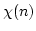 はどうなりますか?
はどうなりますか?



: 行列の対角化
: Dsys
: Dsys
Yasunari SHIDAMA