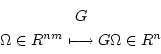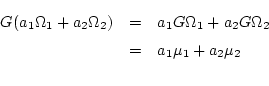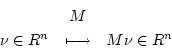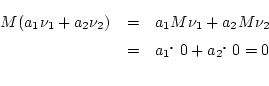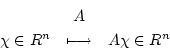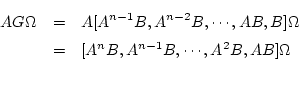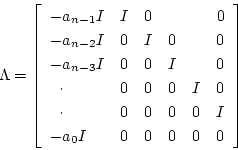: カルマンの分解
: Dsys
: 不変部分空間
大学1年次の線形代数の時間に線形空間の部分空間の話を習ったと思います.
は 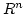 の部分空間です.
の部分空間です.
[証明]
行列 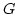 を
を
という写像と見立てると,
集合と写像の話をご存じの方なら
です.
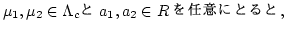
で
ゆえ
従って
[ 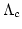 についての証明終り]
行列
についての証明終り]
行列 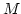 を
を
という写像と見立てると,
これを 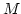 の核
の核 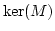 といいます.
といいます.
練習問題11
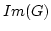 と同様にして,
と同様にして,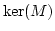 が線形部分空間
であることを示してください.
が線形部分空間
であることを示してください.
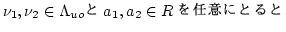
ゆえ,
従って,
――――――――――――――――――――――――――――――――――――――
行列 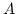 を
を
という写像とみなすと
[証明]
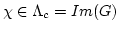 を任意にとると,ある
を任意にとると,ある
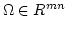 が存在して
が存在して
両辺に 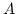 を作用させると
を作用させると
ここで
でしたから
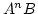 がでてきたので,やっとケーリー・ハミルトンの定理の出番です.
がでてきたので,やっとケーリー・ハミルトンの定理の出番です.
から
よって
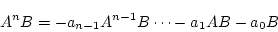 |
(43) |
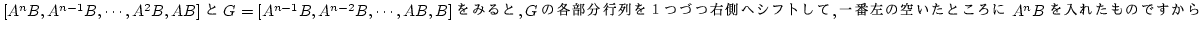
ただし,
結局
よって
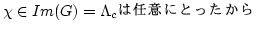
練習問題12
上と同様にして
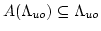 を示してください.
を示してください.



: カルマンの分解
: Dsys
: 不変部分空間
Yasunari SHIDAMA