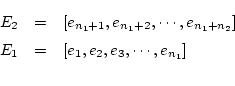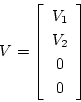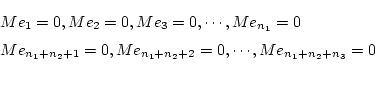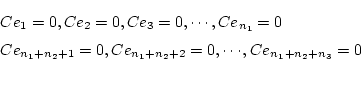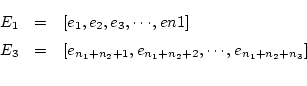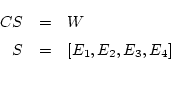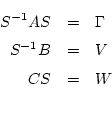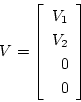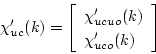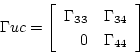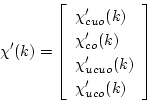

: この文書について...
: Dsys
: 不変部分空間
![$\left [{ 前節までのお話} \right]$](img419.png)
時不変な離散時間線形システムの状態方程式
について

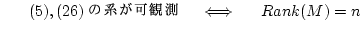
ということが判りました.次にこの可制御性や,可観測性の条件が,充たされない場合
すなわち,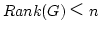 のときや
のときや 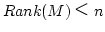 ときはどうなってしまうのか?ということを調べました.
ときはどうなってしまうのか?ということを調べました.
その結果,
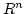 の可制御部分空間
の可制御部分空間
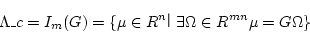 |
(44) |
と,不可観測部分空間
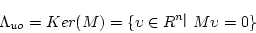 |
(45) |
という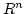 の部分線形空間が定義されました.
の部分線形空間が定義されました.
さらに行列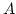 を
を
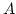
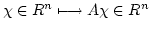
という写像とみなすと
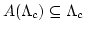
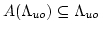
ということが判りました.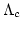 と
と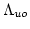 は
は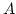 について不変であると言います.
について不変であると言います.
さて,ここからが,この節の本題です.
以後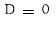 とします.
とします.
まず
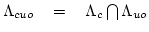 とします.
とします.
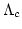 と
と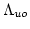 はそれぞれ
はそれぞれ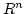 の部分線形空間ですから
の部分線形空間ですから
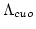 も部分線形空間です.
も部分線形空間です.
![$\left [{ 証明} \right]$](img439.png)
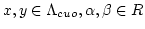 とすれば
とすれば
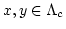 ゆえ
ゆえ
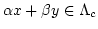
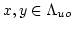 ゆえ
ゆえ
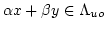
よって
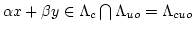
![$\left [{ 証明終り} \right]$](img446.png)
また
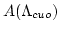
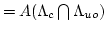
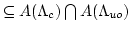
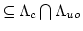
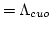
で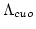 も
も に対して不変.
に対して不変.
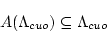 |
(46) |
ここで,線形代数のおさらいです.
―――――――――――――――――――
ベクトル
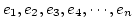 が一次独立
が一次独立
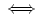 任意の
任意の
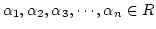 について
について
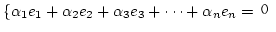 ならば
ならば
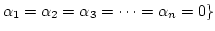
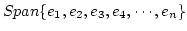
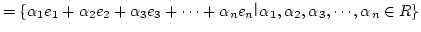
は
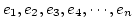 に実数
に実数
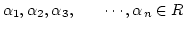 をかけ足しあわせたもの全体の集合で,これ自身,線形空間になっています
をかけ足しあわせたもの全体の集合で,これ自身,線形空間になっています
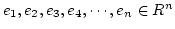 が
が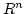 の基底
の基底
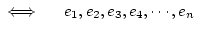 が一次独立でかつ
が一次独立でかつ
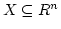 が部分線形空間
が部分線形空間
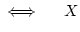 の任意の元
の任意の元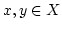 と任意の実数
と任意の実数
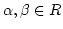 について
について
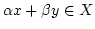
 が部分線形空間のとき
が部分線形空間のとき の基底
の基底
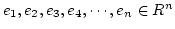
を選べば
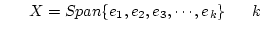 を
を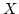 の次元といい
の次元といい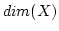 で表す.
で表す.
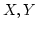 が
が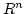 の部分線形空間で
の部分線形空間で
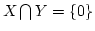 のとき
のとき
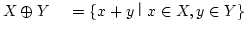
特に  の基底
の基底
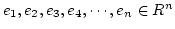 を選べば
を選べば
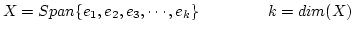
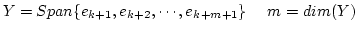
とできる.
―――――――――――――――――おさらい終り――
![$\left [{ 行列Aをスッキリさせる} \right]$](img477.png)
 はそれぞれ
はそれぞれ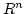 の部分線形空間で,
の部分線形空間で,
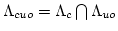
ですから,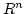 の基底
の基底
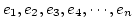 を適当に選べば
を適当に選べば
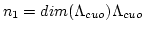 の基底が
の基底が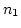 個という意味です.
個という意味です.
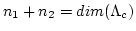
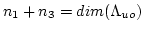
として,下のように,基底
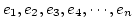 を配分できます.
を配分できます.
可制御部分空間 の基底
の基底
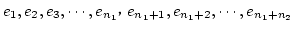
を可制御かつ不可観測な部分空間 の基底
の基底
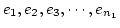
と残りのベクトル
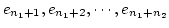 (可制御かつ可観測)
(可制御かつ可観測)
不可制御部分空間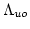 の基底
の基底
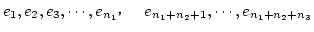
を可制御かつ不可観測な部分空間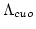 の基底
の基底
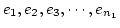
と残りのベクトル
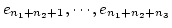 (不可制御かつ可観測)
(不可制御かつ可観測)
上記以外のベクトル
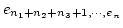 (不可制御かつ可観測)
(不可制御かつ可観測)
すなわち
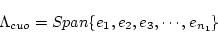 |
(47) |
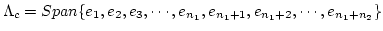
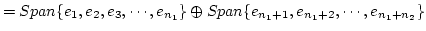
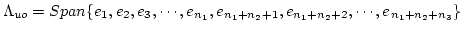
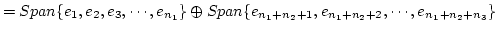
ここで
とすれば
となります.
またそれぞれの部分空間に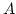 を作用させれば
を作用させれば
です.
まず,
と
に注目します.
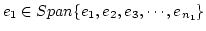 ですから(13)式により
ですから(13)式により
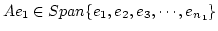
すなわち,ある
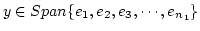 が存在して
が存在して
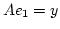
となります.
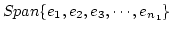 の定義からさらに
の定義からさらに
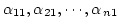 が存在して
が存在して
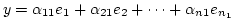 でしたから
でしたから
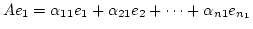
です.ここで
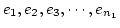 を並べた行列を
を並べた行列を
![$E_1=\left[{e_1,e_2,e_3,\cdots,e_{n_1}}\right]$](img521.png)
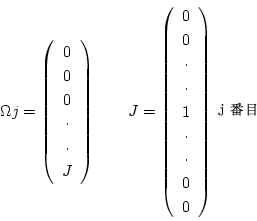
とし,
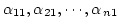 を縦に並べた列ベクトルを
を縦に並べた列ベクトルを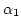 で表せば
で表せば
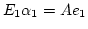
です.
全く同様に
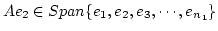 ですから
ですから
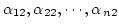 が存在して
が存在して
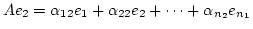
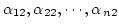 を縦に並べた列ベクトルを
を縦に並べた列ベクトルを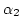 で表せば
で表せば
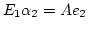
この操作を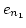 まで繰り返せば,
まで繰り返せば,
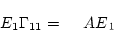 |
(57) |
ただし
![$E_1=\left[{e_1,e_2,e_3,\cdots,e_{n_1}}\right]$](img521.png)
![$\Gamma_{11}=\left[{\alpha_1,\cdots,\alpha_{n_1}}\right]$](img531.png)
次に
について同様な操作により
![$E_2=\left[{e_{n_1+1},e_{n_1+2},\cdots,e_{n_1+n_2}}\right]$](img535.png)
![$E_1=\left[{e_1,e_2,e_3,\cdots,e_{n_1}}\right]$](img521.png)
とすると
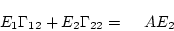 |
(58) |
について同様な操作により
![$E_3=\left[{e_{n_1+n_2+1},e_{n_1+n_2+2},\cdots,e_{n_1+n_2+n_3}}\right]$](img540.png)
とすると
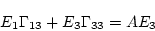 |
(59) |
最後に
について
![$E_4=\left[{e_{n_1+n_2+n_3+1},…,e_n}\right]$](img547.png)
として
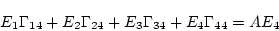 |
(60) |
を得ます.
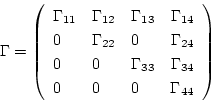
以上をまとめれば
ここで
![$S=\left[{E_1,E_2,E_3,E_4}\right]$](img553.png)
とおくと
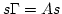
![$S=\left[{E_1,E_2,E_3,E_4}\right]$](img553.png) は基底ベクトルを並べたものですから
は基底ベクトルを並べたものですから
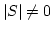 で逆行列
で逆行列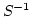 が存在します.
が存在します.
左から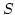 の逆行列
の逆行列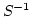 をかければ
をかければ
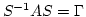
![$\left[{行列Bをスッキリさせる}\right]$](img559.png)
次に行列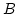 の各列を列ベクトルと見なして
の各列を列ベクトルと見なして
![$B=\left[{b_1,b_2,\cdots,b_m}\right]$](img560.png) と書くと,
と書くと,
![$G=\left[{A^{(n-1)}B,A^{(n-2)}B,\cdots,AB,B}\right]$](img561.png)
ですから
とすると
となり、各 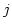 について
について
が判ります。
ここで
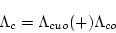 |
(61) |
でしたから行列 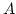 と全く同じ議論によって、
と全く同じ議論によって、
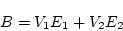 |
(62) |
と書くことができ、
とおくと
が得られます。
で、
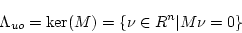 |
(63) |
ですから
です。従って、
でしたから
これは
となることを示しています。
------------
以上をまとめると
「カルマンの分解」
系の方程式
について
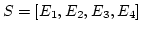 とう変換行列が存在して
とう変換行列が存在して
という変換が可能なことが判りました。
系
系
の としています。
としています。
 と
と
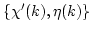 の間には
の間には
によって
と相互に変換できます。系
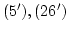 の挙動を調べれば、
系
の挙動を調べれば、
系
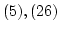 の挙動が判ることになります。
の挙動が判ることになります。
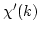 を
を 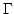 、
、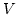 の形に合せて
の形に合せて
と分解します。
さらに 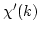 の下半分に着目して
の下半分に着目して
を造ると(1'),(2')から
という式が取り出せます。
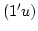 の右辺には制御
の右辺には制御 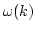 が作用する(作用させる)項がありません。
従って、
が作用する(作用させる)項がありません。
従って、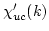 にはいくら努力して制御
にはいくら努力して制御 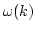 を投じても効果なし
ということになります。箸にかからない。
次に
を投じても効果なし
ということになります。箸にかからない。
次に
によって 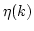 が
が 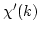 からでてくることになりますが
からでてくることになりますが
ですから、
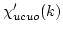 の項はでてきません。
の項はでてきません。
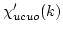 は出力
は出力 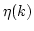 から初期点の推測もできないわけです。
棒にもかからないわけです。 結局
から初期点の推測もできないわけです。
棒にもかからないわけです。 結局
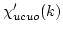 は箸にも棒にもかからない。
は箸にも棒にもかからない。
[練習問題13]
の各要素について、上と同様に説明してください。
[練習問題14]
を示して下さい。


: この文書について...
: Dsys
: 不変部分空間
Yasunari SHIDAMA
![\begin{displaymath}
M=
\left[ \begin{array}{l}
C\\
CA\\
CA^{2}\\
CA^{3}\\
・\\
・\\
CA^{n-1}\\
\end{array} \right]
\end{displaymath}](img425.png)