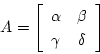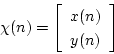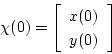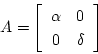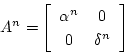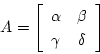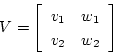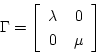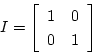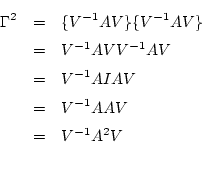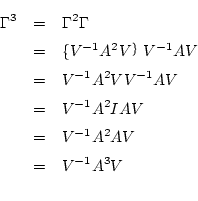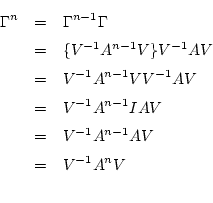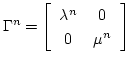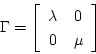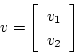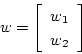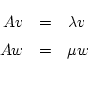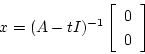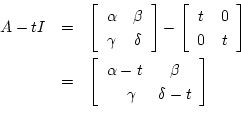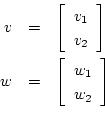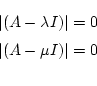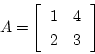

: ジョルダン標準形
: Dsys
: 離散システムの方程式(狼とウサギ)
前節のお話を繰り返しますと.
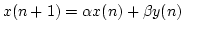 |
|
|
(5) |
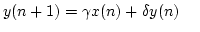 |
|
|
(6) |
という系について行列とベクトルを使えば,
として
 は
は
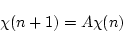 |
(7) |
と表すことができました.
から始めて
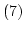 式から
式から
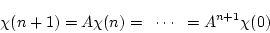 |
(8) |
となります.
前回は手始めに,
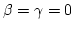 という特別な場合を考えました.
という特別な場合を考えました.
ですから
と簡単に 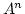 が計算できたわけです.
が計算できたわけです. さて,今度は,
さて,今度は,
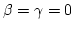 とは限らない一般の場合を考えます.
ここで
とは限らない一般の場合を考えます.
ここで
にある可逆な行列
とその逆行列 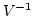 を左右からかけて
を左右からかけて 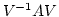 という積を作り,これが
という積を作り,これが
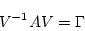 |
(9) |
となったとします.こんな 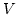 はどうやって探すかという話しは取り合えず置いて,
はどうやって探すかという話しは取り合えず置いて,
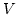 とその逆行列
とその逆行列 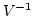 には
には
ただし,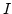 は単位行列
は単位行列
が成り立っていますから
となります.
ここで 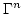 は
は
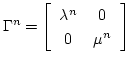 |
|
|
(10) |
と簡単に計算できます.
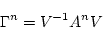 |
(11) |
ですから,両辺に左から 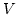 ,右から
,右から 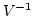 をかけると
をかけると
となります. 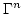 から
から 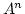 が簡単に計算できます.それで
が簡単に計算できます.それで
となる行列Vを何とか探そうということにします.
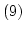 式の両辺に左からVをかけると
式の両辺に左からVをかけると
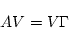 |
(13) |
です. 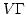 を計算すると
を計算すると
行列 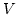 の縦に並んでいる要素をまとめて列ベクトル
の縦に並んでいる要素をまとめて列ベクトル
と書くと,
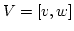 で,
で,
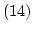 式は
式は
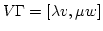 と書けます.すると
と書けます.すると
は,
でさらに左辺を計算すると
両辺の1列目,2列目の列ベクトルは等しいはずですから
という式がでてきます.結局,
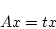 |
(15) |
という定数 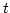 と列ベクトル
と列ベクトル 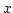 の組2組
の組2組
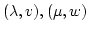 を求める問題になりました.
を求める問題になりました.
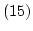 式の右辺は単位行列
式の右辺は単位行列  を使って,
を使って, 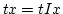 と書けますから,
と書けますから,
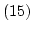 式の右辺を左辺に移項して,
式の右辺を左辺に移項して,
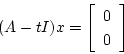 |
(16) |
となります.
実数の1次方程式 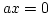 の解は
の解は  の逆数
の逆数 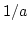 があれば(これは
があれば(これは 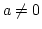 という条件ですが)
という条件ですが)
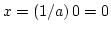 だけです.
同様に,行列
だけです.
同様に,行列 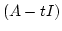 の逆行列
の逆行列 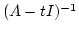 があると,
があると,
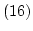 式の両辺に左から
式の両辺に左から 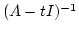 をかけて,
をかけて,
となって
だけが解になってしまいます.これでは目的の 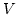 は求まりません.
大学1年次の線形代数の講義を思い出して頂くと,
は求まりません.
大学1年次の線形代数の講義を思い出して頂くと, 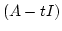 が
逆行列を持たない条件は,
それの行列式について
が
逆行列を持たない条件は,
それの行列式について
でした.実際,これを計算すると,
から 行列式=(左上×右下)−(右上×左下)によって
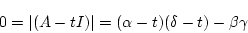 |
(17) |
で 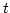 についての2次の代数方程式がでてきます.
まず
についての2次の代数方程式がでてきます.
まず
 式が異なる,2つの実数根を持つ場合について考えます.
この場合,
式が異なる,2つの実数根を持つ場合について考えます.
この場合,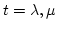 になるわけです.これに対応するベクトル
になるわけです.これに対応するベクトル
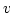 と
と 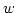 を求めるには,
を求めるには,
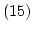 式から
式から
について
として,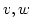 を求めることになります.
を求めることになります.
が成り立っていますから,
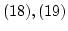 は解は一意には決まりません.
たとえば
は解は一意には決まりません.
たとえば 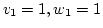 などとすると,
などとすると,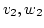 が決まります.
が決まります.
- [ 練習問題 2]

とするとき,上の議論によって,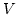 と
と 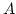 の対角化
の対角化 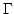 を求めてください.
を求めてください.


: ジョルダン標準形
: Dsys
: 離散システムの方程式(狼とウサギ)
Yasunari SHIDAMA