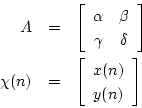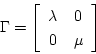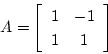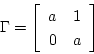: 同値変換の系
: Dsys
: 行列の対角化
で表される系についての議論でした.
(3)式から
となりますが, 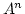 をどう計算するかということになり,
行列
をどう計算するかということになり,
行列 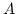 の対角化の話になりました.
の対角化の話になりました.
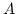 にある行列
にある行列 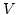 とその逆行列
とその逆行列 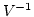 を左右からかけて,
を左右からかけて,
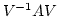 という積を作り,これが
という積を作り,これが
となったとすると(これを 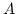 の対角化と言います)
の対角化と言います)
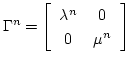 |
|
|
(20) |
で,
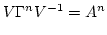 |
|
|
(21) |
となります.
このような 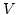 を求めるために,
を求めるために,
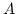 の固有値と固有ベクトルを求める問題
の固有値と固有ベクトルを求める問題
を考えました.
行列式による固有値 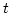 についての2次方程式(これを固有方程式)
についての2次方程式(これを固有方程式)
に2つの異なる実数根 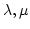 がある場合を扱いました.
今度はこの場合以外を考えます.
がある場合を扱いました.
今度はこの場合以外を考えます.
- (a)
-
まず,方程式(8)が共役複素数根
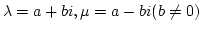 をもつ場合.
この場合は,2つの異なる実数根
をもつ場合.
この場合は,2つの異なる実数根 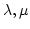 がある場合と同じですが,行列
がある場合と同じですが,行列 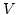 の要素が複素数になります.また
の要素が複素数になります.また 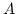 を対角化した行列
を対角化した行列 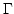 も要素が複素数になります.
実数で表される系(3)式の話しに複素数? と不思議に思われるかもしれませんが,実数の要素だけの行列
も要素が複素数になります.
実数で表される系(3)式の話しに複素数? と不思議に思われるかもしれませんが,実数の要素だけの行列 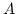 と要素が複素数の行列
と要素が複素数の行列 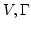 は
は
で関係付けられていて,「帳尻」はあっています.
練習問題3
について,上の式を確認してください.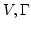 を求めてください.
を求めてください.
- (b)
-
方程式(8)が重根
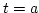 をもつ場合.この場合はAがもとから対角線上にaが並ぶ対角行列である場合と、そうでない場合に分けられます。後者の場合対角化はできませんが,ある
をもつ場合.この場合はAがもとから対角線上にaが並ぶ対角行列である場合と、そうでない場合に分けられます。後者の場合対角化はできませんが,ある 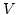 という行列で
という行列で
の形への変換が可能です.(これをジョルダン標準形といいます)
練習問題4
について,上の式を確認してください.この場合 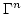 はどうなるでしょうか.
はどうなるでしょうか.



: 同値変換の系
: Dsys
: 行列の対角化
Yasunari SHIDAMA