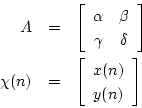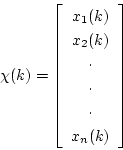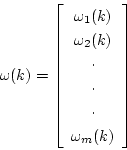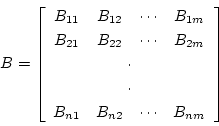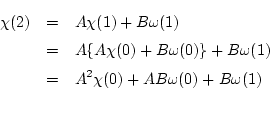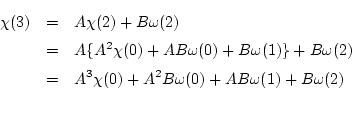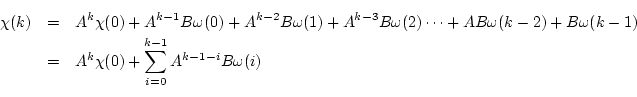: 可制御性
: Dsys
: 同値変換の系
という系の議論でした.
(3)式から
が得られますが,固有方程式 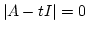 の全ての根
の全ての根 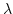 が
が
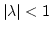 を満たすと,
を満たすと,
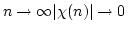 などの性質が判りました.
今度は(3)式に
などの性質が判りました.
今度は(3)式に 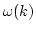 で表現される外部からの強制力が加わった系を考えます.ついでに式を一般化しておきます.今まで
で表現される外部からの強制力が加わった系を考えます.ついでに式を一般化しておきます.今まで  で時間の経過を表す変数にしましたが,これを
で時間の経過を表す変数にしましたが,これを 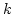 に変えます.
に変えます.
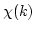 を2次元の列ベクトルから,
を2次元の列ベクトルから, 次元の列ベクトルへ,
次元の列ベクトルへ,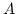 は
は  行
行  列の行列.
新たに加わった
列の行列.
新たに加わった 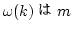 次元の列ベクトルにします.ただし,
次元の列ベクトルにします.ただし,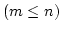
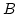 は
は  行
行 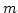 列の行列です.
列の行列です.
新たに加わった外部からの強制力は,人間の意図的な「努力」などを表します.
最初,このお話は草原にいる狼と,ウサギの個体数から出発しましたが,
ウサギや狼の頭数を調整したりする「保護活動」の努力を表すこともあるでしょう.
あるいは,保護と正反対な乱獲や環境破壊かもしれません.
無論,このような方程式は,生態系に限らず,物理系,機械系,社会経済,etcにも現れます.社会経済なら,各年度の政府の経済政策や税制政索を 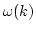 が表すかもしれません.
マイホーム獲得向けての毎年の財形計画や,お子さんの進学のための教育投資や計画かもしれません.
工学では
が表すかもしれません.
マイホーム獲得向けての毎年の財形計画や,お子さんの進学のための教育投資や計画かもしれません.
工学では 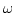 は「制御変数」と呼ばれ
は「制御変数」と呼ばれ 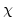 はその時の系の何かの様子を表すので「状態変数」と呼ばれます.
用語の説明は,制御工学やシステム工学の専門書などにお願いするとして,
はその時の系の何かの様子を表すので「状態変数」と呼ばれます.
用語の説明は,制御工学やシステム工学の専門書などにお願いするとして,
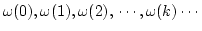 と意図的な外力(制御)を加えていくと,
と意図的な外力(制御)を加えていくと,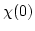 から始まる
から始まる
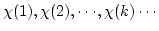 はどうなるか調べてみます.
まず(5)式から
はどうなるか調べてみます.
まず(5)式から
です.次にこれと(5)式から
さらに
結局
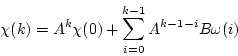 |
(22) |
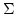 記号の中の式では
記号の中の式では 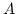 のべき乗の指数と
のべき乗の指数と 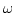 の括弧の中の数字が,その和が
の括弧の中の数字が,その和が 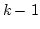 となるように変化しています.このような演算は畳み込み演算と呼ばれます.
いまは
となるように変化しています.このような演算は畳み込み演算と呼ばれます.
いまは 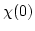 から
から 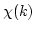 へと計算しましたが,
へと計算しましたが, 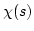 から始めて
から始めて
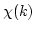 までなら
までなら
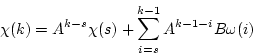 |
(23) |
となります.



: 可制御性
: Dsys
: 同値変換の系
Yasunari SHIDAMA