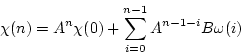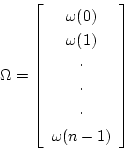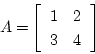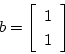: 可観測性
: Dsys
: 状態方程式
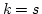 から
から 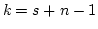 まで(5)式の系に何らかの
まで(5)式の系に何らかの  個の制御量
個の制御量
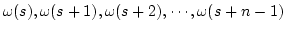 を加えて任意の
を加えて任意の 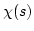 から出発して
から出発して
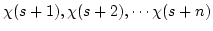 と変化させ,最後の
と変化させ,最後の 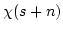 がある目標の
がある目標の 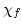 と等しくなるようにできるかどうかを考えます.これが可能な場合,系(3)は「可制御」であるといいます.
状態変数のベクトルの次元数
と等しくなるようにできるかどうかを考えます.これが可能な場合,系(3)は「可制御」であるといいます.
状態変数のベクトルの次元数  と同じ数の
と同じ数の  個必要です.
政府の
個必要です.
政府の  ヵ年計画が成功するかどうかとか,
ヵ年計画が成功するかどうかとか,  年後に目的を達成するような,政策立案が可能かといった問題です.あるいは,お子様への
年後に目的を達成するような,政策立案が可能かといった問題です.あるいは,お子様への  ヵ年教育計画で,目標の学校受験のための学力向上の努力かもしれません.
結果は同じですので
ヵ年教育計画で,目標の学校受験のための学力向上の努力かもしれません.
結果は同じですので 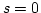 とします.(23)式の
とします.(23)式の 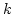 に
に  を入れると
を入れると
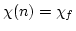 となるようにしたいわけで,また最初の
となるようにしたいわけで,また最初の 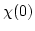 は変えることができませんから,
は変えることができませんから,
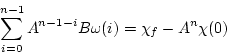 |
(24) |
となります.
この式を満足する
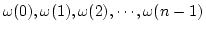 があるか? という問題です.
があるか? という問題です.
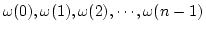 はそれぞれ
はそれぞれ 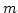 次元の列ベクトルですが,これを縦に並べて
次元の列ベクトルですが,これを縦に並べて
という 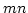 次元の列ベクトルを作り,
次元の列ベクトルを作り,
 個の
個の  行
行 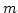 列の
列の
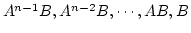 を横に並べて
を横に並べて
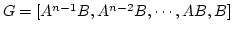 という
という  行
行 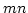 列の行列を作ると,
(8)式は
列の行列を作ると,
(8)式は
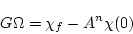 |
(25) |
という方程式です.未知数のベクトルが 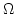 で寸法が
で寸法が 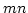 ,係数の行列
,係数の行列 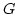 が
が  行
行 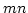 列で,
列で, 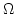 のうち
のうち 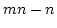 個分だけ自由度があります.この方程式が解を持つためには
「
個分だけ自由度があります.この方程式が解を持つためには
「 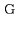 の階数が
の階数が  」という条件 (
」という条件 ( 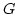 の
の  行
行  列の正方な部分行列のどれかの行列式の
値が
列の正方な部分行列のどれかの行列式の
値が 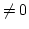 ) ということが条件です.
これを
) ということが条件です.
これを
と書きます.すなわち
ここでは,判りやすくするために 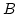 を
を  行1列の行列,つまり,
行1列の行列,つまり,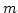 次元の列ベクトル
次元の列ベクトル 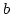 としてみます.この場合,
としてみます.この場合,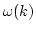 はベクトルではなく数になります.
(1次元列ベクトルですから)
はベクトルではなく数になります.
(1次元列ベクトルですから)
すると
は  行
行  列の正方行列になります.
すると(25)を満足するための
列の正方行列になります.
すると(25)を満足するための 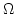 があるためには,
があるためには, 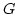 の行列式
の行列式 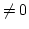 です.
即ち
です.
即ち
練習問題6
について可制御性を判定してください.
この場合は 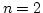 です.
です.



: 可観測性
: Dsys
: 状態方程式
Yasunari SHIDAMA