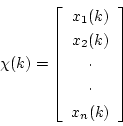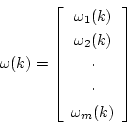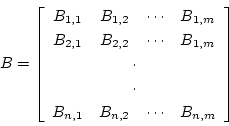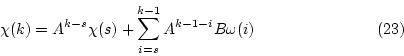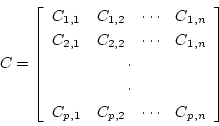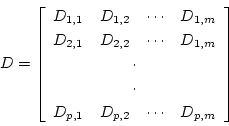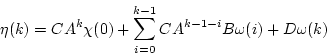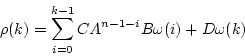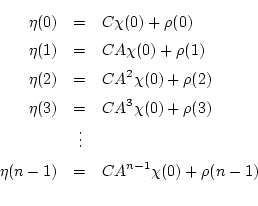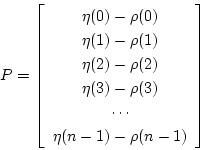

: ケーリー・ハミルトンの定理
: Dsys
: 可制御性
今までのお話は
のお話で,
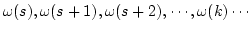 と意図的な外力(制御)を加えていくと,
と意図的な外力(制御)を加えていくと, 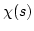 から始まる
から始まる
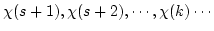 はどうなるか調べてみました.
結局
はどうなるか調べてみました.
結局
となります.
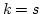 から
から 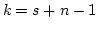 まで(5)式の系に何らかの
まで(5)式の系に何らかの 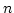 個の制御量
個の制御量
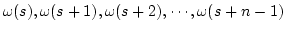 を加えて任意の
を加えて任意の 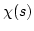 から出発して
から出発して
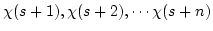 と変化させ,最後の
と変化させ,最後の 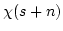 がある目標
の
がある目標
の 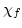 と等しくなるようにできるかどうかを考えます.これが可能な場合,系(5)は「可制御」であるといいます.このための条件は
と等しくなるようにできるかどうかを考えます.これが可能な場合,系(5)は「可制御」であるといいます.このための条件は
でした.
ここで 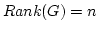 すなわち「
すなわち「 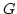 の階数が
の階数が 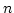 」という条件は
」という条件は
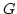 の
の 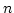 行
行 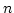 列の正方な部分行列のどれかの行列式の
値が
列の正方な部分行列のどれかの行列式の
値が 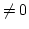 ということが条件でした.
さて(5)式の系に
ということが条件でした.
さて(5)式の系に
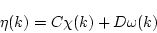 |
(26) |
という式を加えます.
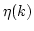 は
は 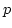 次の列ベクトル,
次の列ベクトル,
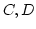 はそれぞれ
はそれぞれ 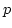 行
行 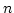 列の行列,
列の行列, 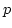 行
行 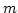 列の行列です.
列の行列です.
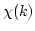 が系の状態変数と呼ばれるのに対して,
が系の状態変数と呼ばれるのに対して,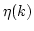 は系の出力と呼ばれます.
は系の出力と呼ばれます.
を時不変な離散時間線形システムの状態方程式と呼びます.
「時不変」というのは,係数行列 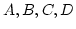 が時間に(
が時間に( 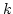 に)
依存しない定数行列だからです.「線形」というのは(5),(26)が
に)
依存しない定数行列だからです.「線形」というのは(5),(26)が
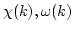 について線形(係数行列
について線形(係数行列 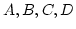 がそれぞれ
掛け合わされ,加えられている)という意味です.
がそれぞれ
掛け合わされ,加えられている)という意味です.
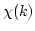 をお子様の学力,
をお子様の学力, 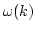 を進学準備のための教育の投資・努力に例えましたが,
を進学準備のための教育の投資・努力に例えましたが,
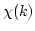 が学力の要素「計算能力」「読解力」「論理思考能力」etcなどを表し,
が学力の要素「計算能力」「読解力」「論理思考能力」etcなどを表し,
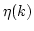 は学期末テストの(総合)得点などに例えられます.
教育の投資・努力
は学期末テストの(総合)得点などに例えられます.
教育の投資・努力 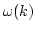 によって変化するのは学力
によって変化するのは学力 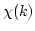 ですが,これが目に見えて確認できる(観測できる)のは学期末テストの(総合)得点などの
ですが,これが目に見えて確認できる(観測できる)のは学期末テストの(総合)得点などの
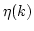 で,
で, 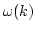 は学力
は学力 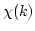 を経由して
を経由して  という行列によって間接的に
という行列によって間接的に
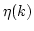 をもたらしていることになります.無論
をもたらしていることになります.無論 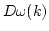 のように直接
のように直接
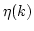 に影響する項もありますが.
に影響する項もありますが.
- [親子の会話]
- 教育ママ(または教育パパ)
- 「XXX君,ちっとも成績良くならないね!!勉強してるの?」
=「
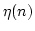 が上がらないね,
が上がらないね,
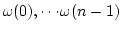 は?」
は?」
- 覚めた子供
- 「そんなこと言ったって,ちゃんと勉強(努力)してきたよ.でもパパ達の子供
だものしょうがないでしょ」
=「
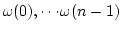 はちゃんと与えた,そもそも初期点
はちゃんと与えた,そもそも初期点 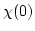 が悪い.」
が悪い.」
家庭内の会話は兎も角:
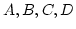 と
と
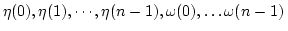 から
から 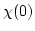 を決定する
にはどのような条件が必要でしょうか?
を決定する
にはどのような条件が必要でしょうか? 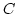 が正方行列で逆行列
が正方行列で逆行列 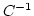 があれば
があれば
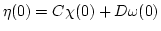 から
から
で直ぐに判るのですが, 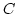 は一般には,そうではありません.
は一般には,そうではありません.
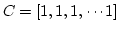 という横ベクトルで
という横ベクトルで 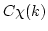 がその
がその 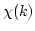 の成分の総和
(
の成分の総和
( 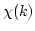 が
が 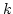 年後の[国語,数学,英語,物理,化学,生物]の学力,
年後の[国語,数学,英語,物理,化学,生物]の学力,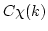 が総合得点
ということもあるでしょう.)
テストの得点は基礎学力の投影であっても,それだけで,基礎学力を正確に知ることは出来ません.
これには(5),(26)を再度見てみる必要があります.
が総合得点
ということもあるでしょう.)
テストの得点は基礎学力の投影であっても,それだけで,基礎学力を正確に知ることは出来ません.
これには(5),(26)を再度見てみる必要があります.
次に
で,
でしたから
同様に
で
でしたから
さらに
で
でしたから
この操作を繰り返せば,
結局
とおくと
を得て,これを見やすいように変形して
ここで 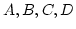 と
と
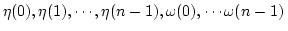 が全て
判っていますから
が全て
判っていますから
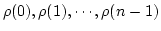 も既知な量です.
も既知な量です.
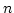 個の
個の 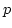 行
行 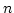 列の行列
列の行列
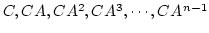 を縦に並べ
を縦に並べ 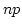 行
行 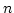 列の行列
列の行列
と 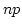 次の列ベクトル
次の列ベクトル
を作ると(27)式は
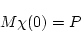 |
(28) |
となります.
方程式(28)が解を持つ条件は
です.
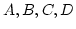 と
と
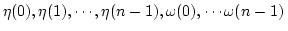 から
から 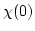 を決定できる場合,この系は可観測であるといいます.
特に
を決定できる場合,この系は可観測であるといいます.
特に 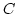 が1次の横ベクトルの場合(この場合,出力
が1次の横ベクトルの場合(この場合,出力 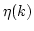 はベクトルでなく数)は,この条件は
はベクトルでなく数)は,この条件は
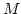 の行列式
の行列式 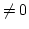 と同値です.
今までの議論をまとめると
時不変な離散時間線形システムの状態方程式
と同値です.
今までの議論をまとめると
時不変な離散時間線形システムの状態方程式
について
ただし,
ただし,
練習問題7
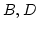 も適当な行列とします.
この系の可観測性を判定してください.
この場合は
も適当な行列とします.
この系の可観測性を判定してください.
この場合は 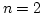 です.
です.


: ケーリー・ハミルトンの定理
: Dsys
: 可制御性
Yasunari SHIDAMA