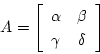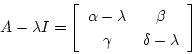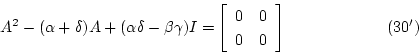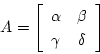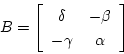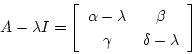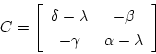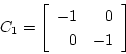

: 不変部分空間
: Dsys
: 可観測性
資源の「リサイクル」は今日的課題ですが,この節では,行列の「リサイクル」の話
をします.
これは次節のお話の準備です.
行列 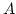 の固有値を求め,
の固有値を求め, 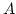 の対角化を行いましたが,そのとき用いた
特性方程式
の対角化を行いましたが,そのとき用いた
特性方程式
については,他の性質も知られています.
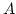 が
が 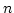 次の正方行列なら
次の正方行列なら
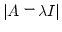 は
は 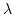 についての最高次が
についての最高次が
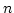 次の多項式になります.すなわち
次の多項式になります.すなわち
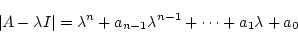 |
(29) |
例
なら
で
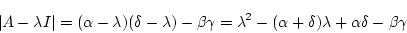 |
(30) |
です.
ここで(29)の 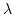 の替わりに
の替わりに 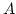 を使った行列の式も
を使った行列の式も
を充たします.
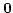 は要素が全て
は要素が全て 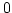 の行列です.
の行列です.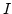 は単位行列です.
これをケイリー・ハミルトンの定理といいます.
実際,(30)のついて
は単位行列です.
これをケイリー・ハミルトンの定理といいます.
実際,(30)のついて 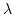 の替わりに
の替わりに 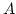 を使った式を調べると
を使った式を調べると
練習問題8 (30')を確認してください.
以下この定理を証明します.
[ケーリー・ハミルトンの定理の証明]
[準備:余因子行列]
大学の1年次か高校時代,行列の逆行列の話と一緒に,余因子行列を習ったと思います.
 |
(31) |
について 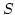 の余因子行列
の余因子行列 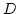 は
は
 |
(32) |
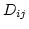 は
は 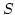 の第
の第 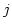 行と第
行と第 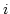 列の要素を除いた
列の要素を除いた
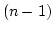 行
行 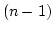 列の部分行列式
列の部分行列式
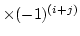 です.
例えば
です.
例えば
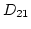 は
は 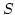 の第2行と第1列の要素を除いた
の第2行と第1列の要素を除いた 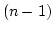 行
行 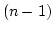 列の部分行列
列の部分行列
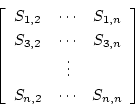 |
(33) |
の行列式 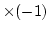 です.
例
です.
例
なら  の余因子行列
の余因子行列  は
は
さて, 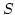 と
と 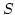 の余因子行列
の余因子行列 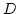 との積には
との積には
という関係があります.
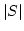 は
は 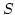 の行列式,
の行列式, 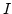 は単位行列です.
は単位行列です.
練習問題9 上の, 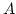 と
と 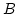 の例について確認してください.
[定理の証明]
行列
の例について確認してください.
[定理の証明]
行列 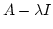 の余因子行列を
の余因子行列を 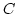 とします.
このとき
とします.
このとき 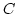 の
の 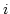 行
行 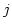 列の要素は
列の要素は 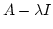 の第
の第 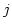 行と第
行と第 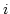 列の要素を除いた
列の要素を除いた 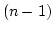 行
行 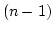 列の部分行列式
列の部分行列式
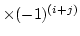 ですので
ですので 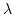 についての最高次数
についての最高次数 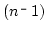 次式です.
これが
次式です.
これが 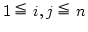 つ いて成立っていますから,
つ いて成立っていますから, 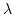 の各次数ごとに整理すると
の各次数ごとに整理すると
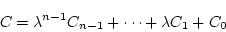 |
(34) |
となります.
[例]
の例では,これの余因子行列 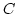 は
は
で
とおくと
[例終わり]
さて,行列とその余因子列の積=行列式ですから
これに(29)式
(34)式
を代入すると
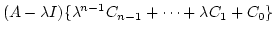 |
| |
|
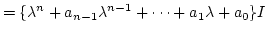 |
(35) |
(35)式の両辺の 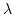 の次数を比較して,
の次数を比較して,
[証明終わり]
この定理から,
であり,
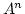 は
は
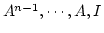 から計算できます.すると,結局,
から計算できます.すると,結局,
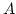 の
の 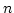 以上のべき乗は,
以上のべき乗は,
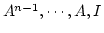 から計算できることが判ります.
練習問題10
から計算できることが判ります.
練習問題10
について,証明の議論をやってみてください.


: 不変部分空間
: Dsys
: 可観測性
Yasunari SHIDAMA