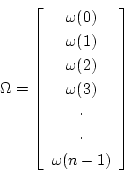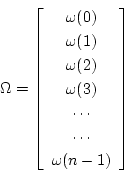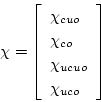

: 不変部分空間
: Dsys
: ケーリー・ハミルトンの定理
まず今までのお話のおさらいをします.
時不変な離散時間線形システムの状態方程式
について調べてきました.
初期点 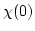 から
から 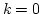 から
から 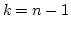 まで(5)式の系に何らかの
まで(5)式の系に何らかの 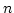 個の制御量
個の制御量
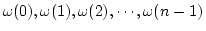 を加えた場合
を加えた場合 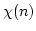 は
は
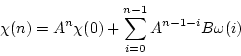 |
(41) |
となります.
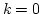 から
から 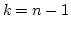 まで(5),(26)式の系に何らかの
まで(5),(26)式の系に何らかの 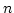 個の制御量
個の制御量
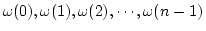 を加えて
任意の
を加えて
任意の 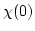 から出発して
から出発して
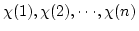 と変化させ,
最後の
と変化させ,
最後の 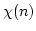 がある目標の
がある目標の 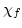 と等しく
なるようにできる場合,系(5),(26)は「(完全)可制御」であるといいます.このための条件は
と等しく
なるようにできる場合,系(5),(26)は「(完全)可制御」であるといいます.このための条件は
でした.
また, 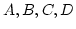 と
と
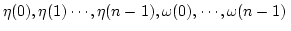 から
から 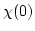 を決定することができるというのが可観測性でした.
を決定することができるというのが可観測性でした.
ただし,
でした.
[ケーリー・ハミルトンの定理]
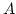 の特性方程式を
の特性方程式を
とするとき:
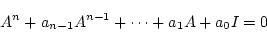 |
(42) |
が成立っていました.
以上が今までのおさらいです.
さて,そもそも制御性の条件は(41)式を行列 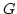 を使って
を使って
と変形し,
任意の
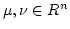 に対し
に対し
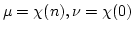 として
として
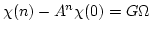 を充たす
を充たす 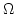 が存在する条件を求めました.
が存在する条件を求めました.
上で,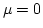 にとった
にとった
を可制御性
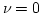 にとった,
にとった,
を可到達性と言います.
可制御性は任意に与えられた初期点 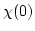 から原点へ動かせる
から原点へ動かせる 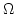 が存在するかどうか,
可到達性は原点から任意に与えられた点
が存在するかどうか,
可到達性は原点から任意に与えられた点 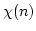 へ動かせる
へ動かせる 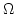 が存在するかどうか,です.
以後,議論を簡単にするため
が存在するかどうか,です.
以後,議論を簡単にするため 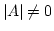 とします.これは
とします.これは 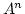 の逆行列が存在することを意味し,この場合は,
の逆行列が存在することを意味し,この場合は,
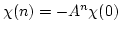 が解けることになり,
可制御性と可到達性は同値になります.
用語の解説は,専門の教科書にお願いするとして,今後,可制御性(=可到達性)
が解けることになり,
可制御性と可到達性は同値になります.
用語の解説は,専門の教科書にお願いするとして,今後,可制御性(=可到達性)
を考察します.
この場合も
です.
[箸にも棒にもかからぬ]
これからが本題です.可制御性や,可観測性の条件が,充たされない場合
すなわち,
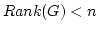 のときや
のときや 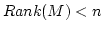 ときはどうなってしまうのか?
ということです.
ときはどうなってしまうのか?
ということです.
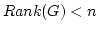 の場合どんなに
の場合どんなに
を選んでも 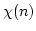 の選び方によっては
の選び方によっては
が充たされないということが起きてしまいます.
( 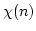 に到達できないわけです.)
「成せばなる,成さねば成らぬ何事も,成らぬは人の成さぬなり」
(クリントン前米国大統領も,尊敬したという上杉鷹山)
なんて言ってられなくなります.
に到達できないわけです.)
「成せばなる,成さねば成らぬ何事も,成らぬは人の成さぬなり」
(クリントン前米国大統領も,尊敬したという上杉鷹山)
なんて言ってられなくなります.
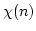 で,系がこの
で,系がこの 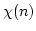 に,
に,
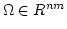 を選べば到達できるものすなわち
を選べば到達できるものすなわち
を充たす, 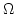 が存在するも全体を
が存在するも全体を
で定義します.
可制御部分空間なんて名前があるのですが,箸にかかる要素の集合とでも呼びます.
可観測性の条件についても,同様なことが起きます.
そもそも可観測性の条件は,既に判っている系の係数行列 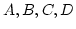 と
系に加えた制御
と
系に加えた制御
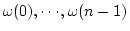 と
それによる出力
と
それによる出力
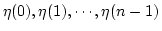 から
造られるベクトル
から
造られるベクトル 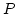 と
と 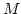 による方程式
による方程式
が 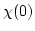 について解けるかどうかの条件でした.
について解けるかどうかの条件でした.
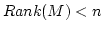 の場合,
の場合,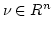 について
について 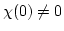 で
で
となることが起きます.
ですから 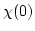 が
が 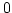 と区別できなくなります.
このような
と区別できなくなります.
このような 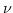 の集合を,
の集合を,
で定義します.不可観測部分空間などと呼ぶのですが,棒にもかからない集合
とでも呼びます.
系の方程式
は状態変数 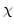 の要素を4つに分け
の要素を4つに分け
と表現することにより,4つのパーツに分解することができます.
「カルマンの分解」


: 不変部分空間
: Dsys
: ケーリー・ハミルトンの定理
Yasunari SHIDAMA