

: この文書について...
: ネットワーク集合上の最小化問題
: ネットワーク集合上の最小化問題
この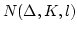 が
が の有界閉集合と同様な性質をもっていることを示します。
の有界閉集合と同様な性質をもっていることを示します。
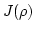 はこの
はこの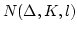 から
から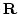 への写像
への写像
として扱います。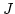 には連像性が要求されます。先ず,
には連像性が要求されます。先ず,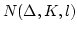 には距離が定義されます。
には距離が定義されます。
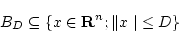 |
(4.3) |
から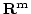 への連続関数
全体の集合
への連続関数
全体の集合
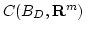 の部分集合ですが,
の部分集合ですが,
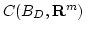 には
には
が定義されています。ここで,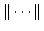 は
は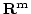 の
ベクトル
の
ベクトル
に対して
で定義されます。
上記の距離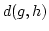 は
は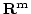 の距離同様,以下の性質を充たしています。
の距離同様,以下の性質を充たしています。
このような距離が定義される集合を距離空間と言います。
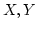 が距離
が距離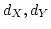 が定義されている距離空間とします。
が定義されている距離空間とします。
定義 4.2.1
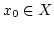
とし、
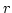
を正の数と
するとき、
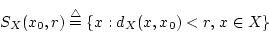 |
(4.4) |
で定義される
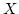
の部分集合
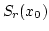
を中心が
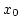
で半径が
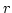
の開
球といいます。
無論,距離空間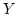 でも,開球が定義されます。
でも,開球が定義されます。
定義 4.2.2
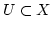
として,
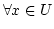
に対して、
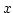
を中心とする十分小さい開球
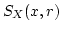
を
とり,
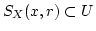
となるようにできるとき、
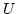
を
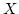
の開集合であ
るといいます。
(証明)
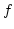 が
が 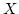 で連続で、
で連続で、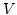 を
を 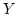 の開集合と仮定して、
の開集合と仮定して、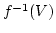 が
が 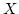 の開集合となることを証明します
。
の開集合となることを証明します
。
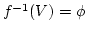 なら,これは開集合です。そこで、
なら,これは開集合です。そこで、
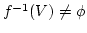 とします。
とします。
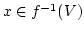 とすると、
とすると、 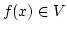 である。
である。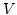 は開集合で
あるから、
は開集合で
あるから、 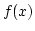 を中心とする開球
を中心とする開球
が存在します。 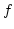 は連続ですから,開球
は連続ですから,開球
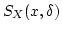 が存在して,
が存在して,
以上より、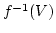 は開集合です。
は開集合です。
( )
)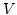 が
が 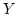 の任意の開集合ならば、常に
の任意の開集合ならば、常に
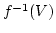 が
が 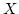 の開集合であると仮定します。
の開集合であると仮定します。
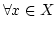 とし,
とし, 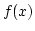 を中心とする任意の開球
を中心とする任意の開球
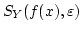 をとります。
をとります。
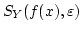 は開集合ですから,仮定よりその逆像
は開集合ですから,仮定よりその逆像 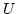 は開集合で
は開集合で 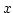 を含む。よって,定義により
を含む。よって,定義により
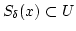 が存在します。
が存在します。
よって、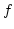 は点
は点 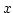 で連続になります。
で連続になります。
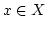 は任意でしたから,
は任意でしたから, 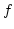 は
は 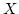 で連続です。
で連続です。
定義 4.2.4
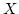
を距離空間とします。
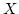
の開集合の
集合
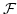
,これを開集合族と言いますが,
が
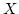
の部分集合
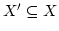
を覆っているとき,すなわち,
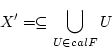 |
(4.6) |
となっているとき,
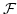
を
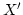
の開被覆といいます。
定義 4.2.5
距離空間
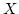
の部分集合
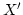
に任意の開被覆
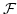
が与えられたとき、それから適当な有限個
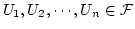
を選んで
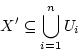 |
(4.7) |
とできるとき,
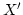
はコンパクト集合であるといいます。
コンパクト集合の例としては,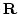 の閉区間
の閉区間![$[a,b]$](img205.gif) またそれの
またそれの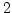 重直積
重直積
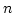 重直積
重直積
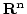 の閉球の閉球
の閉球の閉球
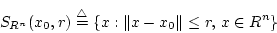 |
(4.8) |
があります。
さて,連続写像とコンパクト集合の関係については以下が知られています。
定理 4.2.3
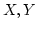
が距離空間とする。
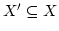
がコンパクトで写像
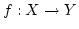
が連続ならば、
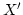
の像
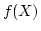
はコンパクトである。
証明
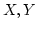 が距離
が距離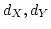 が定義されている距離空間とします。
が定義されている距離空間とします。
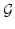 を
を 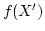 の開被覆とすると,
開集合の連続写像による逆像は開集合ですので,
の開被覆とすると,
開集合の連続写像による逆像は開集合ですので,
は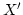 の開被覆です。
の開被覆です。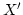 はコンパクトでしたから
これから有限個
はコンパクトでしたから
これから有限個
を選んで, 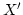 を覆うことができます。すなわち,
を覆うことができます。すなわち,
そうすると、
となり、
が 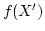 の有限個の部分開被覆となって、
の有限個の部分開被覆となって、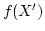 がコンパクト集合であることがわかります。
がコンパクト集合であることがわかります。
また,以下の定理も知られています。
定理 4.2.4
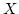
を距離空間とする。
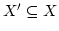
がコンパクトならば,
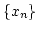
を
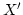
の任意の無限列とすると
き,
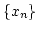
の無限部分列
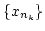
と
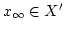
が存在して
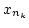
は
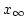
に収束する。
上の二つの定理を用いて,
定理 4.2.5
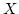
を距離空間とする。
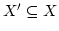
がコンパクトで写像
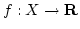
が連続ならば、
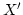
上での像
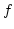
は最大・最小値をもつ。
証明
まず,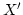 の像
の像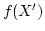 は
は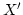 がコンパクトで、
がコンパクトで、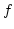 が連続写像なので,
が連続写像なので,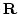 のコンパクト集合です。
のコンパクト集合です。
そこで,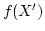 の上限,下限
の上限,下限
をとると,それぞれ,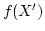 の元の無限点列
の元の無限点列
が存在して,
です。
ここで,
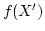 はコンパクト集合でしたから,
はコンパクト集合でしたから,
の部分点列
と,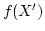 の元
の元
が存在して,
です。
実数列とその部分列の極限は一致するので,
で,結局,
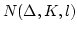 のコンパクト性について述べてます。
のコンパクト性について述べてます。
定理 4.2.6
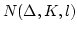
は有界閉集合
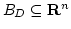
上の連続関数
全体
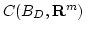
の部分集合として,コンパクトである。
- (証明)
-
結合係数のベクトル
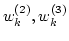 と、しきい値
と、しきい値
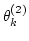 及びシグモイド関数の最大勾配
及びシグモイド関数の最大勾配 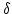 による多重対
による多重対
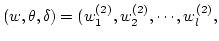 |
| |
|
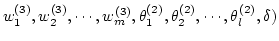 |
(4.9) |
から 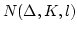 の元
の元 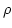 への対応が
への対応が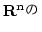 コンパクト集合
コンパクト集合
![$[-K,K]^{2l+m} \times [0,\Delta ]$](img239.gif) から
から 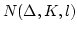 の上への写
像
の上への写
像
![\begin{displaymath}
\Omega :[-K,K]^{2l+m} \times [0,\Delta ] \to N(\Delta,K,l)
\end{displaymath}](img240.gif) |
(4.10) |
を定義していることが判ります。
コンパクト集合の連続写像による像はコンパクト集合であるから、この全写 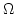 が連続写像であることを示せばよいわけです。
そこで
が連続写像であることを示せばよいわけです。
そこで
![$[-K,K]^{2l+m} \times [0,\Delta ]$](img239.gif) の別の元として結合係数
の別の元として結合係数
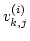 としきい値
としきい値 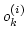 及びシグモイド関数の最大勾配
及びシグモイド関数の最大勾配
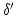 による多重対
による多重対
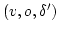 をとり、これに
をとり、これに  により
により
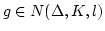 が対応するものとする。すなわち、
が対応するものとする。すなわち、
 式と同様に
式と同様に
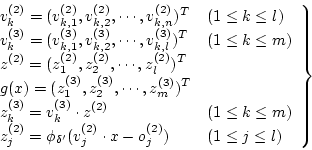 |
(4.11) |
とします。
ここで
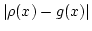 を評価します。
を評価します。
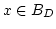 について
について 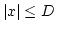 が成り立つから
が成り立つから
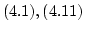 式により
式により
です。また 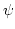 は有界でしたから
は有界でしたから
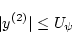 |
(4.13) |
ただし
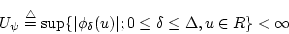 |
(4.14) |
これから、
を得ます。結局、任意の 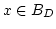 について
について
ただし、
を得ます。従って
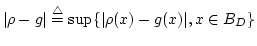 |
| |
|
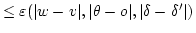 |
(4.17) |
が成り立ちます。
であるから写像 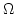 は連続写像です。すなわち
は連続写像です。すなわち
![$N(\Delta,K,l) = \Omega([-K,K]^{2l+m}\times [0,\Delta])$](img270.gif) はコンパ
クト集合です。
はコンパ
クト集合です。
この命題によって、シグモイド関数の最大勾配と結合係数、しきい値がそれ
ぞれある正数  以下の階層型ネットワークのクラスを表す
関数集合
以下の階層型ネットワークのクラスを表す
関数集合 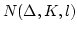 は
は
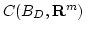 内でそのコンパクト性
が保証されます。
内でそのコンパクト性
が保証されます。
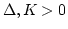 を十分大きくとればよく用いれている殆どの階層型ネットワ
ークがこの集合に含まれると考えてよいでしょう。
を十分大きくとればよく用いれている殆どの階層型ネットワ
ークがこの集合に含まれると考えてよいでしょう。
ここで
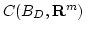 で連続関数
で連続関数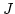
についての最小化問題が解を持つとします。
前節の定理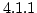 によれば,
によれば,
が成立っています。そこで,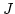 の
の
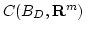 上での連続性から
上での連続性から
ところで各
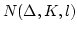 には最小化元が存在するので、
結局
には最小化元が存在するので、
結局
一方
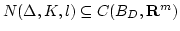 ゆえ
ゆえ
です。したがって
とります。
ところで、 について
について
なので
が得られ,したがって
これは中間層の素子数  を十分大きくとり
を十分大きくとり
 内の最小化元を求めれば
内の最小化元を求めれば
の近似が得られることを示しています。


: この文書について...
: ネットワーク集合上の最小化問題
: ネットワーク集合上の最小化問題
Yasunari SHIDAMA
![]() が
が![]() の有界閉集合と同様な性質をもっていることを示します。
の有界閉集合と同様な性質をもっていることを示します。
![]() はこの
はこの![]() から
から![]() への写像
への写像
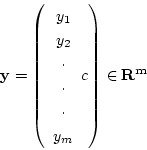
![]() は
は![]() の距離同様,以下の性質を充たしています。
の距離同様,以下の性質を充たしています。

![]() が距離
が距離![]() が定義されている距離空間とします。
が定義されている距離空間とします。
を中心とする任意の半径
の開球
に対し、
を中心とする半径
の開 球
が存在し、
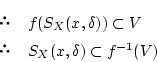
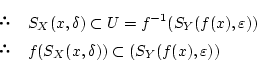
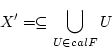
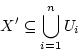
![]() の閉区間
の閉区間![]() またそれの
またそれの![]() 重直積
重直積
![]() が距離
が距離![]() が定義されている距離空間とします。
が定義されている距離空間とします。
![]() を
を ![]() の開被覆とすると,
開集合の連続写像による逆像は開集合ですので,
の開被覆とすると,
開集合の連続写像による逆像は開集合ですので,
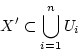
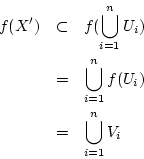
![]() の上限,下限
の上限,下限
![]() のコンパクト性について述べてます。
のコンパクト性について述べてます。
![]() と、しきい値
と、しきい値
![]() 及びシグモイド関数の最大勾配
及びシグモイド関数の最大勾配 ![]() による多重対
による多重対
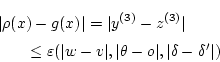
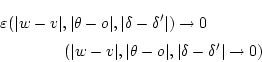
![]() 以下の階層型ネットワークのクラスを表す
関数集合
以下の階層型ネットワークのクラスを表す
関数集合 ![]() は
は
![]() 内でそのコンパクト性
が保証されます。
内でそのコンパクト性
が保証されます。
![]() を十分大きくとればよく用いれている殆どの階層型ネットワ
ークがこの集合に含まれると考えてよいでしょう。
を十分大きくとればよく用いれている殆どの階層型ネットワ
ークがこの集合に含まれると考えてよいでしょう。
![]() で連続関数
で連続関数![]()
![]() によれば,
によれば,

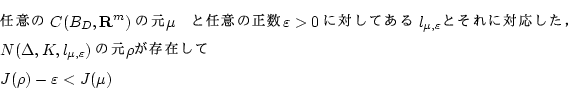
![]() には最小化元が存在するので、
結局
には最小化元が存在するので、
結局
![]() について
について