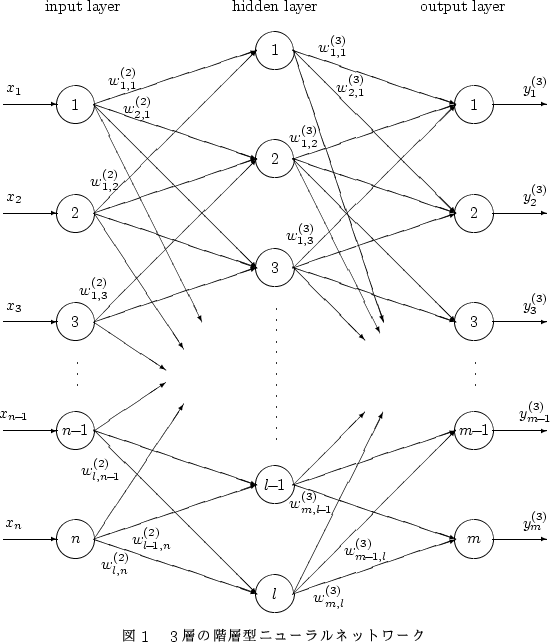
以下は3層の階層型ニューラルネットワークの例を図示したものです。
このニューラルネットワークの第1層(input layer)、第2層(hidden layer)、
第3層(output layer)の素子数はそれぞれ ![]() 個である。第
個である。第 ![]() 層の
層の
![]() 番の素子から第
番の素子から第 ![]() 層
層 ![]() 番の素子への結合係数は
番の素子への結合係数は
![]() で表しています。
で表しています。
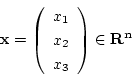
このニューラルネットワークは![]() 次元空間
次元空間![]() の元
の元
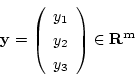
具体的にどう
各
![]() に対し,第
に対し,第![]() 層は
層は![]() 個の細胞(図中の○印)を持つものとすると,
第
個の細胞(図中の○印)を持つものとすると,
第![]() 層第
層第![]() 細胞の出力
細胞の出力![]() は
は
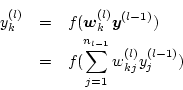
荷重
![]() を変化させれば,この階層型ネットワークが望ましい出力を出すように調整できます。
を変化させれば,この階層型ネットワークが望ましい出力を出すように調整できます。
例えば,こうして得られたシステムの出力
![]() と出力すべき値
と出力すべき値
![]() との2乗誤差を
との2乗誤差を
![]() として,すなわち出力信号
として,すなわち出力信号
![]() に対し
に対し
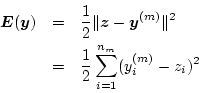
修正には,![]() が上のネットワークに使われる荷重のベクトル
が上のネットワークに使われる荷重のベクトル![]() について2階微分可能ならば,
について2階微分可能ならば,
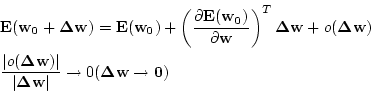
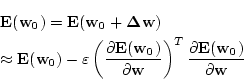
次節で説明するBP法は,そのような手法の一つで,
![]() について最急降下法を用いて
について最急降下法を用いて
![]() を変化させるものです。
を変化させるものです。
![]() の有界な領域上の任意の連続関数が,このようなニューラルネットワークによって任意の精度で近似できることも知られています。(
の有界な領域上の任意の連続関数が,このようなニューラルネットワークによって任意の精度で近似できることも知られています。(![]() や
や ![]() )
これについては,後の章で述べます。
)
これについては,後の章で述べます。