- (1)
- 節点の集合
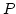
- (2)
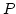 の点の順序対
の点の順序対
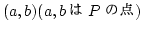 の集合
の集合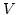
からなります。
![]() のとき
のとき
![]() です。また
です。また
![]() は
は![]() の自乗直積
の自乗直積
![]() の部分集合です。 すなわち,
の部分集合です。 すなわち,
順序対![]() は向きのついた枝,あるいは弧と呼ばれ,
は向きのついた枝,あるいは弧と呼ばれ,
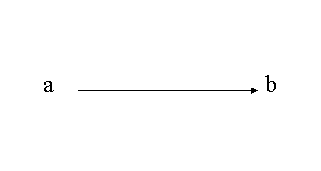
(図5.1)
のように表すことができます。![]() は始点,
は始点,![]() は終点と呼ばれます。
このような枝のまたは弧の図をつなぎ合わせば,有向グラフ
は終点と呼ばれます。
このような枝のまたは弧の図をつなぎ合わせば,有向グラフ
![]() を平面図で表すことができます。
を平面図で表すことができます。
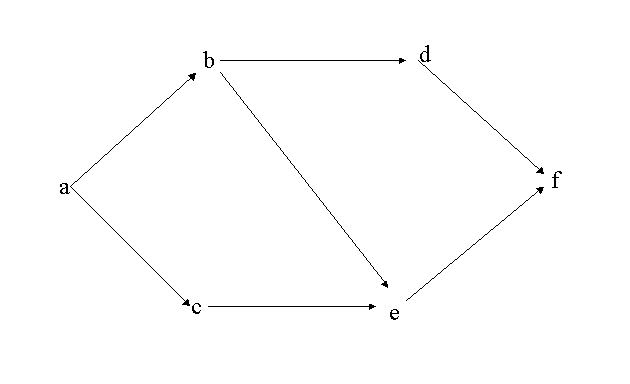
(図5.2)
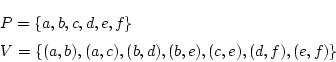
有向グラフ![]() の弧には,長さや,所要時間などのデータでラベル付けされているとき
の弧には,長さや,所要時間などのデータでラベル付けされているとき
![]() をラベル付き有向グラフといいます。
をラベル付き有向グラフといいます。
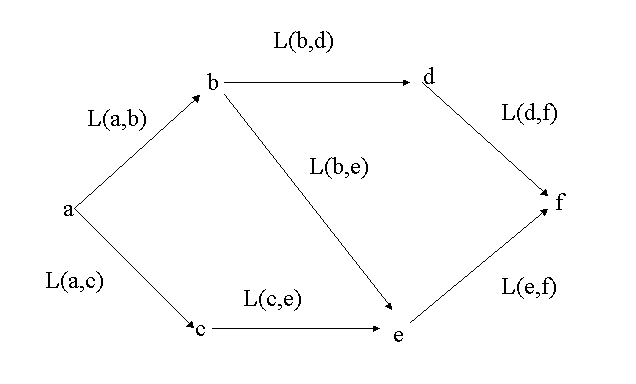
(図5.3)
節点の多重対
![]() で,各
で,各
![]() が
が![]() の元,すなわち弧であるものを
路といいます。
の元,すなわち弧であるものを
路といいます。
上の図では,
![]() などが路です。
などが路です。
![]() をラベル付き有向グラフとします。ただし,
をラベル付き有向グラフとします。ただし,
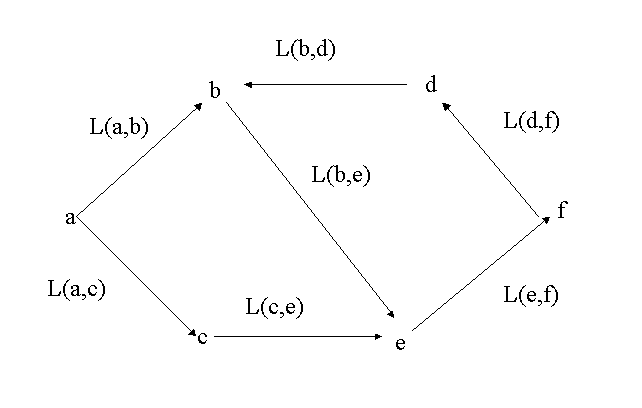
(図5.4)
の![]() のように「閉じた路」は含まないものとします。
のように「閉じた路」は含まないものとします。
さて,簡単にするため、集合![]() が
が![]() 個の節点からなっているとして
個の節点からなっているとして
![]() とし,夫々の弧に付けられている,ラベルはその弧の長さを
表すものとしておきます。
とし,夫々の弧に付けられている,ラベルはその弧の長さを
表すものとしておきます。
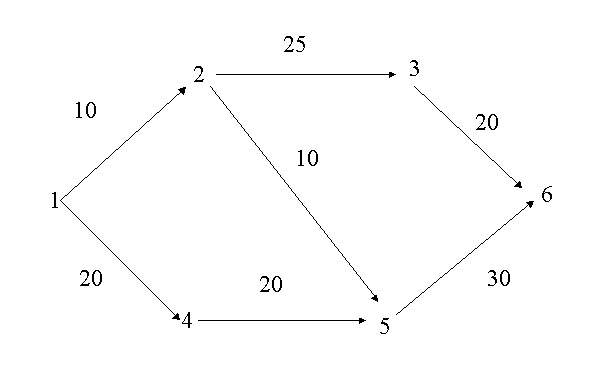
(図5.5)
弧をつなぎ合わせて作られる路の長さは,それを構成している弧の長さの和で
表します。例えば(図5)で路![]() の長さは,
の長さは,![]() で
で![]() です。
です。
節点1から出発して,節点nへ行くための長さ最小の路をどう求めるかという問題を考えます。(図5.5)の例では,路(1,2,5,6)が解で,長さ![]() です。
です。
![]() の点の数が少なければ,路を全て調べてみるのも一つの方法ですが,数が多くなると
実用的ではありません。
の点の数が少なければ,路を全て調べてみるのも一つの方法ですが,数が多くなると
実用的ではありません。