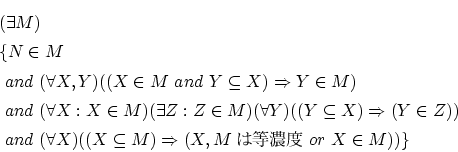Tarskiの公理

以下は,証明なしの定理として書かれていますがTarskiの公理として 知られるものです。集合$N$が与えられたときに, $N$をその要素として含む集合$M$が存在して

1. $X \in M$かつ$Y \subseteq X$ならば$Y \in M$となる。
2. $X \in M$に対して,$Y \subseteq X$となる$Y$は 全て$Y \in Z$となる　$Z \in M$が存在する。
3. $X \subseteq M$ならば,$X$と$M$は等濃度かあるいは, $X \in M$

という条件を充たすという主張です。

theorem
   ex M st N in M &
     (for X,Y holds X in M & Y c= X implies Y in M) &
     (for X st X in M ex Z st Z in M & for Y st Y c= X holds Y in Z) &
     (for X holds X c= M implies X,M are_equipotent or X in M);

記号論理で書けば,

$$\begin{eqnarray*} &&(\exists M)\\ && \{N \in M \\ && \ and \ (\forall X,... ... \subseteq M) \Rightarrow (X,M は等濃度 \ or\ X \in M) ) \} \end{eqnarray*}$$