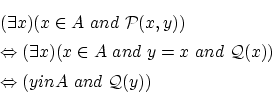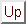


: 合弁と共通部分
: 集合の演算
: 集合の演算
目次
集合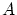 が集合
が集合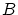 に含まれることは
に含まれることは
で定義します。
同様に
集合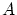 が
が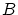 に等しいことは外延性の公理で定義されています。再度書くと
に等しいことは外延性の公理で定義されています。再度書くと
で定義します。
特に空集合についてはその存在公理
から
こような集合が2つあったとすると,それらを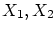 として
として
から
が成立ち,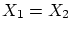 となり,一意性が成立っています。そこで,このような集合を
となり,一意性が成立っています。そこで,このような集合を
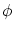 で表します。
で表します。
また,
任意の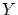 について
について
から
以下の命題が成り立っています。
- 命題2.1.1
- 証明
- ラッセルのパラドクス
-
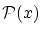 を
を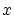 についての関係式とします。
についての関係式とします。
で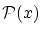 を充たす
を充たす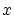 すべての集合というの表現がよく用いられますが,
これを不用意に用いると次のような問題が生じます。
すべての集合というの表現がよく用いられますが,
これを不用意に用いると次のような問題が生じます。
- 病的な集合の定義
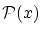 として
として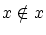 をとります。
をとります。
そして
とします。
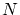 を
を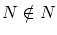 とすると:
とすると:
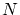 の定義により,この集合に属する条件を充たしますから,
の定義により,この集合に属する条件を充たしますから,
よって
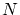 を
を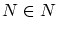 とすると:
再び,
とすると:
再び,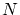 の定義により,この集合に属するための条件により
の定義により,この集合に属するための条件により
よって
公理から
は恒に成立っていますから,上の場合分けの方法によって,
が成立ってしまいます。
パラドクスが生じてしまいます。 ・・・ラッセルのパラドックス
- このラッセルのパラドックスを避けるにはどうしたらよいでしょうか?
一つの解決策は表記法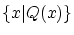 が認められるのは,条件式
が認められるのは,条件式
が成立するときのみとすることです。
前の例において
が認められるとすると
ここで
は成り立たないので、矛盾が生じます。従って
は認められないというようにです。
- 関係式
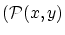 について
について
が成立つとき,
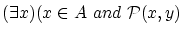 を
を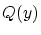 とおけば
とおけば
第1章で述べた置換の推論規則
によって
が成立ち,この基準が充たされます。
よって
という集合を定義することができます。
- (分出の定理)
関係式
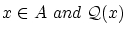 についても,
についても,
という集合を定義することができます。
[証明]
関係式
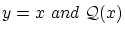 を
を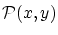 とおけば
とおけば
のとき,
よって
よって,
ここで,
よって
が成立ちます。
[証明終]



: 合弁と共通部分
: 集合の演算
: 集合の演算
目次
Yasunari SHIDAMA
![]() が集合
が集合![]() に含まれることは
に含まれることは
![]() が
が![]() に等しいことは外延性の公理で定義されています。再度書くと
に等しいことは外延性の公理で定義されています。再度書くと
![]() について
について
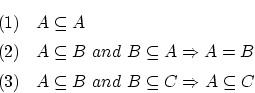

![]() を
を![]() についての関係式とします。
についての関係式とします。
![]() を
を![]() とおけば
とおけば
![]() を
を![]() とおけば
とおけば