


: 逆写像
: 集合の基礎的性質その2−2
: 目次
目次
写像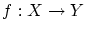 について
について
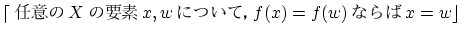 を満たすとき
を満たすとき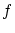 は一対一(
は一対一( または単射)であるといいます.
または単射)であるといいます.
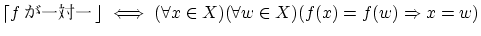
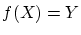 を満たすとき
を満たすとき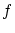 は全射
は全射 (または
(または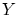 の上への写像)であるといいます.
の上への写像)であるといいます.
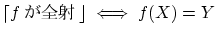
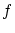 が単射かつ全射であるとき双射(または全単射)といいます.
が単射かつ全射であるとき双射(または全単射)といいます.
問題
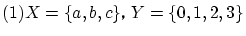 とします.
とします.
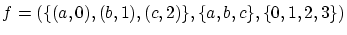 は単射の例ですが,他の例を作っ下さい.
は単射の例ですが,他の例を作っ下さい.
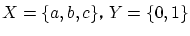 とします.
とします.
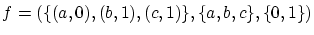 は全射の例ですが,他の例を作っ下さい.
は全射の例ですが,他の例を作っ下さい.
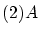 と
と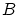 を
を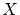 の部分集合とします.写像
の部分集合とします.写像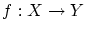 が単射のとき
が単射のとき
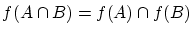 を示して下さい.
を示して下さい.
以上を命題としてまとめておきます.
![$\left[ {命題3.2.1} \right] $](img18.png)
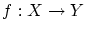 のとき
のとき
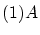 と
と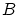 が
が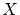 の部分集合なら
の部分集合なら
特に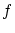 が単射なら
が単射なら
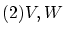 が
が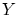 の部分集合
の部分集合
Yasunari SHIDAMA
![]()
![]() のとき
のとき
![]() と
と![]() が
が![]() の部分集合なら
の部分集合なら