


: 関係の形式的定義
: 集合の基礎的性質その3
: 目次
目次
今まで,写像(関数)の形式的定義を紹介しました.
これはXからYへの写像(のグラフ)を,直積集合X×Yの部分集合として扱う方法でした.
写像は
で定義されました.
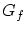 は
は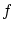 のグラフで直積集合
のグラフで直積集合
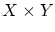 の部分集合です.
の部分集合です.
今後,
のように
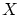 の要素
の要素
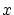 に対して対応する
に対して対応する
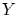 の要素が具体的に与えられている場合は,写像の表現
の要素が具体的に与えられている場合は,写像の表現
の替わりに,
あるいは
と表します.
写像と同様に,直積集合の部分集合で定義できるものとして,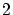 項関係があります.
項関係があります.
「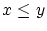 」
とか「
」
とか「
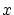 と
と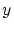 は
は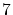 を法として同値」といった二つの変数に関する関係です.
これを形式化して扱うのにも直積集合を使います.
を法として同値」といった二つの変数に関する関係です.
これを形式化して扱うのにも直積集合を使います.
Yasunari SHIDAMA
![]() 」
とか「
」
とか「
![]() と
と![]() は
は![]() を法として同値」といった二つの変数に関する関係です.
これを形式化して扱うのにも直積集合を使います.
を法として同値」といった二つの変数に関する関係です.
これを形式化して扱うのにも直積集合を使います.