


: 命題計算の完全性定理
: 命題論理の公理系
: 演繹定理
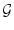 を
を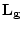 の部分集合の論理式の集合
の部分集合の論理式の集合
とする。
を簡単のため,
と書くことにする。
ある論理式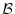 が存在して
が存在して
となるとき,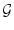 は矛盾するという。
このような
は矛盾するという。
このような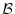 が存在しないとき,
が存在しないとき,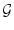 は無矛盾であるという。
は無矛盾であるという。
- 定理6
-
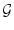 が矛盾すれば,すべての論理式は公理系
が矛盾すれば,すべての論理式は公理系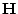 と
と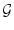 から証明可能である。すなわち任意の論理式
から証明可能である。すなわち任意の論理式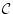 について
について
- 証明
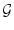 が矛盾すれば,ある論理式
が矛盾すれば,ある論理式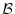 が存在して
が存在して
である。ここで
公理 によれば任意の論理式
によれば任意の論理式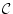 について
について
であり,
推論規則「論理積」によれば,
も証明可能である。
従って,
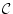 も証明可能になる。
も証明可能になる。
Yasunari SHIDAMA
![]() も証明可能になる。
も証明可能になる。