| (3.25) |
| (3.25) |
![]() は
は
![]() のどれかと一致するはずであるから
のどれかと一致するはずであるから![]() としておく。
としておく。
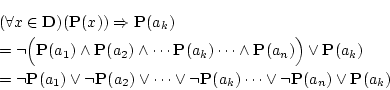
| (3.26) |
| (3.27) |
| (3.28) |
| (3.29) |
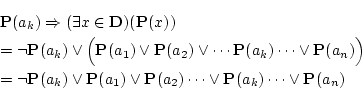
| (3.30) |
よって任意の対象 ![]() に対し
に対し
| (3.31) |
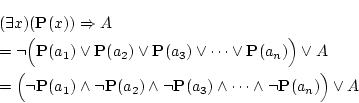
| (3.32) | |||
| (3.33) |
| (3.34) |
| (3.35) |
| (3.36) |
| (3.37) |
| (3.38) |
| (3.39) |
| (3.40) |
| (3.41) |
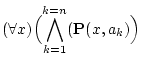 |
|||
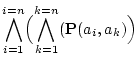 |
|||
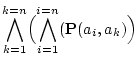 |
|||
| (3.42) |
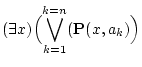 |
|||
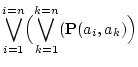 |
|||
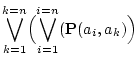 |
|||
| (3.43) |
すなわち,ひき続いて現れる同種の限定記号の順序を変えても変わりない。
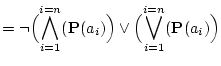 |
(3.44) |
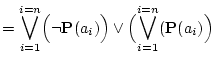 |
|||
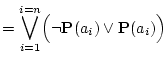 |
|||
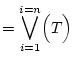 |
|||
| (3.45) |
| (3.46) |
| (3.47) |
| (3.48) |
| (3.49) |
は恒真論理式である。
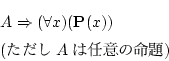
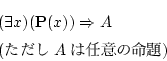
たとえば,