を追加してできる新たな系で 論理式
| (4.5) |
| (4.6) |
を追加してできる新たな系を
を追加してできる系を
| (4.7) |
| (4.8) |
| (4.9) |
| (4.10) |
- (1).
 は
は
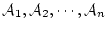 のうち1つで
ある。
のうち1つで
ある。
- (2).
 は
は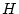 の各公理の形の論理式である。
の各公理の形の論理式である。
- (3).
- 論理式
 の前に論理式
の前に論理式 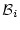 と
と
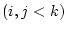 があり,
があり, は
は
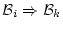 の
形をしている。
の
形をしている。
- (4).
- 論理式
 の前に論理式
の前に論理式 
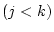 があり,
があり, は
は
であり,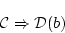
(4.11)  は
は
の形をしている。 ただし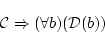
(4.12) 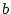 は自由変数記号で
は自由変数記号で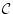 には現れないものとする。
には現れないものとする。
- (5).
- 論理式
 の前に論理式
の前に論理式 
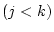 があり,
があり, は
は
であり,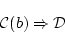
(4.13)  は
は
の形をしている。 ただし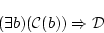
(4.14) 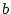 は自由変数記号で
は自由変数記号で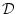 には現れないものとする。
には現れないものとする。
| (4.15) |
| (4.16) |
| (4.17) |
実際,
- (1).
 が
が
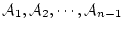 のうち1つであれば,
のうち1つであれば,
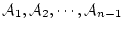 は
は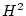 では公理であるから
証明可能な論理式ゆえ推論規則「添加」
では公理であるから
証明可能な論理式ゆえ推論規則「添加」
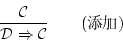
により,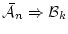 は
は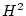 で証明可能な論理式になる。
で証明可能な論理式になる。
 が
が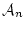 自身ならば,公理
自身ならば,公理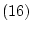 を
を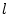 回適用して
回適用して
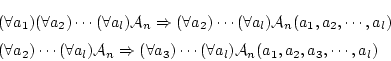
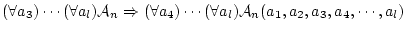
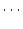
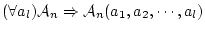
により,
は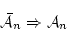
(4.18) 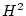 で証明可能な論理式である。
で証明可能な論理式である。
- (2).
 が
が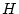 の各公理の形の論理式であるとき,
同様に「添加」により,
の各公理の形の論理式であるとき,
同様に「添加」により,
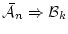 は
は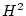 で証明可能な論理式である。
で証明可能な論理式である。
- (3).
- 論理式
 の前に論理式
の前に論理式 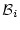 と
と
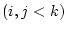 があり,
があり, は
は
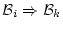 の
形をしているときは,
の
形をしているときは,
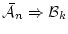 の前に,
の前に,
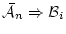 と
と
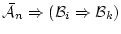 とがあることになる。
これに「複推移」
とがあることになる。
これに「複推移」
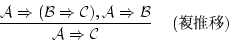
を適用すると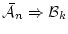 が証明可能であることが
示される。
が証明可能であることが
示される。
- (4).
- 論理式
 の前に論理式
の前に論理式 
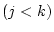 があり,
があり, は]
は]
であり,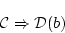
(4.19)  は
は
の形をしている場合。 ただし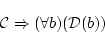
(4.20) 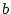 は自由変数記号で
は自由変数記号で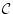 には現れないものとする。
この場合,
には現れないものとする。
この場合,
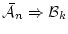 の前に,
の前に,
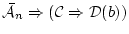 があり,
があり,
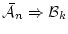 は
は
の形をしている。 ここで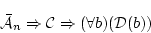
(4.21) 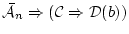 に全称化の推論規則
に全称化の推論規則
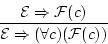
を適用して
が証明可能である。また公理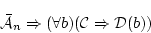
(4.22) 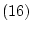 から
から
が証明可能である。 全称化の推論規則によれば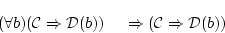
(4.23)
が証明可能である。以上を連鎖させれば,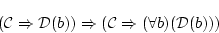
(4.24)
が証明可能であることが わかる。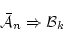
(4.25)
最後に, - (5).
- 論理式
 の前に論理式
の前に論理式 
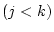 があり,
があり, は
は
であり,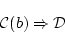
(4.26)  は
は
の形をしている場合を考えよう。 ただし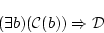
(4.27) 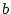 は自由変数記号で
は自由変数記号で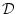 には現れないものとする。
には現れないものとする。
この場合,
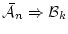 の前に,
の前に,
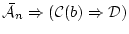 があり,
があり,
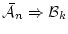 は
は
の形である。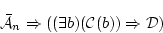
(4.28) 先ず,公理
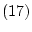 によれば
によれば
が証明可能である。これと既に証明可能なことが分かっている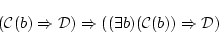
(4.29) 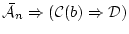 を連鎖させれば,
を連鎖させれば,
が証明可能なことが分かる。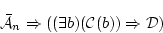
(4.30) 
特に
![]() についての全称化を行わずに
についての全称化を行わずに
| (4.31) |
| (4.32) |
定理![]() と同様に
体系
と同様に
体系![]() についてその公理系に論理式
についてその公理系に論理式
を追加してできる新たな系を
を追加してできる系を
| (4.33) |
| (4.34) |
| (4.35) |
が
- (1).
 は
は
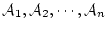 のうち1つで
ある。
のうち1つで
ある。
- (2).
 は
は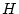 の各公理の形の論理式である。
の各公理の形の論理式である。
- (3).
- 論理式
 の前に論理式
の前に論理式 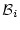 と
と
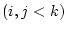 があり,
があり, は
は
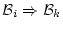 の
形をしている。
の
形をしている。
- (4).
- 論理式
 の前に論理式
の前に論理式 
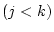 があり,
があり, は
は
であり,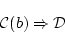
(4.36)  は
は
の形をしている。 ただし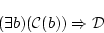
(4.37) 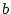 は自由変数記号で
は自由変数記号で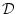 には現れないものとする。
には現れないものとする。
| (4.38) |
実際,
- (1).
 が
が
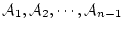 のうち1つであれば,
のうち1つであれば,
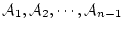 は
は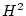 では公理であるから
証明可能な論理式ゆえ推論規則「添加」
では公理であるから
証明可能な論理式ゆえ推論規則「添加」
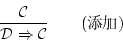
により,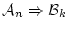 は
は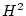 で証明可能な論理式になる。
で証明可能な論理式になる。
 が
が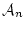 自身ならば,公理
自身ならば,公理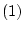 により,
により,
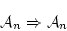
は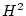 で証明可能な論理式である。
で証明可能な論理式である。
- (2).
 が
が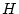 の各公理の形の論理式であるとき,
同様に「添加」により,
の各公理の形の論理式であるとき,
同様に「添加」により,
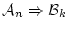 は
は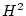 で証明可能な論理式である。
で証明可能な論理式である。
- (3).
- 論理式
 の前に論理式
の前に論理式 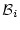 と
と
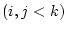 があり,
があり, は
は
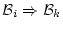 の
形をしているときは,
の
形をしているときは,
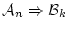 の前に,
の前に,
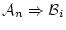 と
と
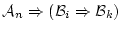 とがあることになる。
これに「複推移」
とがあることになる。
これに「複推移」
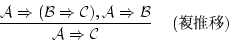
を適用すると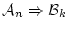 が証明可能であることが
示される。
が証明可能であることが
示される。
最後に,
- (4).
- 論理式
 の前に論理式
の前に論理式 
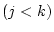 があり,
があり, は
は
であり,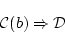
(4.39)  は
は
の形をしている場合を考えよう。 ただし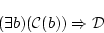
(4.40) 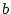 は自由変数記号で
は自由変数記号で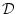 には現れないものとする。
には現れないものとする。
この場合,
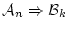 の前に,
の前に,
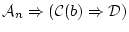 があり,
があり,
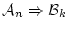 は
は
の形である。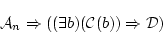
(4.41) 先ず,公理
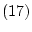 によれば
によれば
が証明可能である。これと既に証明可能なことが分かっている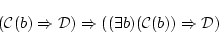
(4.42) 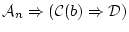 を連鎖させれば,
を連鎖させれば,
が証明可能なことが分かる。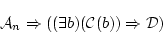
(4.43) 