![]() と
と ![]() の双対性を使って例えば
の双対性を使って例えば
「集合の体(field of sets) ![]() とは,次の性質(1)-(3)を満たす集合である:
(1)
とは,次の性質(1)-(3)を満たす集合である:
(1) ![]() (2)任意の
(2)任意の ![]() について,
について,
![]() (3) 任意の
(3) 任意の ![]() について,
について,
![]() 」
」
- 1.
-
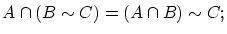
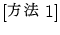 記号論理の規則は既知なものとします。
記号論理の規則は既知なものとします。
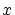 を任意にとると:
を任意にとると:
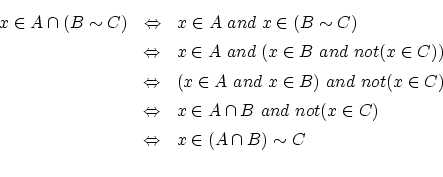
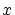 は任意にとったから
は任意にとったから
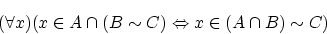
よって
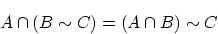
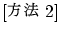
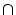 と
と 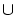 と補集合
と補集合 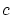 の集合演算は既知としてよいなら
ただし,補集合は
の集合演算は既知としてよいなら
ただし,補集合は 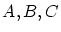 を部分集合としてふくむ含適当な
集合上での補集合をとるものとして
を部分集合としてふくむ含適当な
集合上での補集合をとるものとして
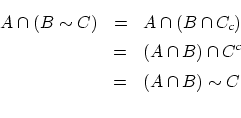
以下、取り合えず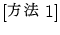 のようにします.
のようにします.
- 2.
-
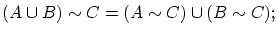
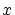 を任意にとると:
を任意にとると:
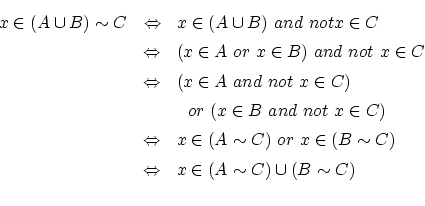
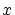 は任意にとったから
は任意にとったから
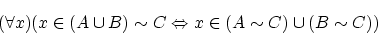
よって
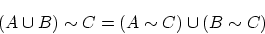
- 3.
-
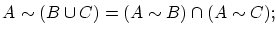
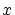 を任意にとると:
を任意にとると:
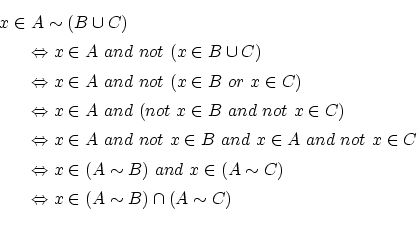
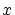 は任意にとったから
は任意にとったから
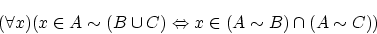
よって
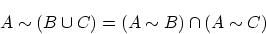
- 4.
-
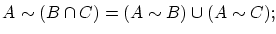
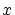 を任意にとると:
を任意にとると:
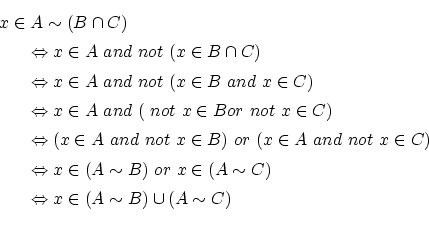
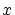 は任意にとったから
は任意にとったから
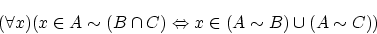
よって
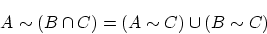
- 5.
-
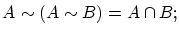
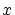 を任意にとると:
を任意にとると:
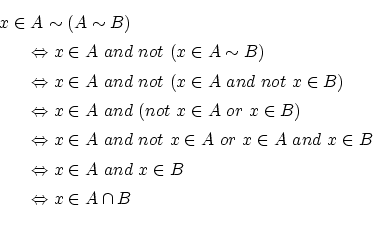
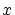 は任意にとったから
は任意にとったから
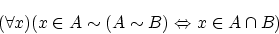
よって
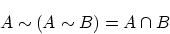
- 6.
-
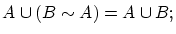
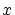 を任意にとると:
を任意にとると:
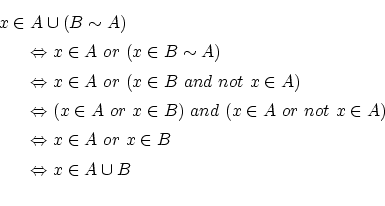
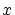 は任意にとったから
は任意にとったから
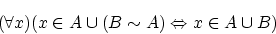
よって
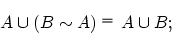
- 7.
-
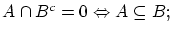
[証明] 以下で,補集合は
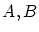 を含むある集合
を含むある集合 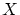 について考えるこ
とにします.
について考えるこ
とにします.
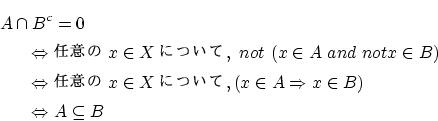
または以下による.
右辺を仮定すれば
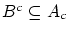 により
により
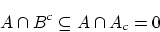
また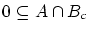 は常に成り立っているから
は常に成り立っているから
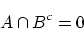
左辺を仮定すれば
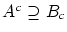 より
より
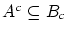
すなわち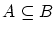
- 8.
-
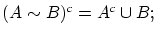
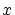 を任意にとると:
を任意にとると:
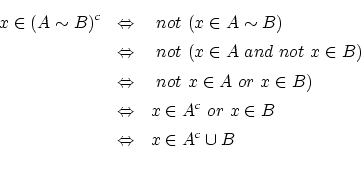
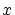 は任意にとったから
は任意にとったから
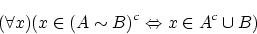
よって
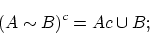
- 9.
-
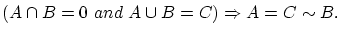
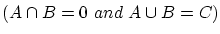 を仮定し
を仮定し
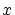 を任意にとると:
を任意にとると:
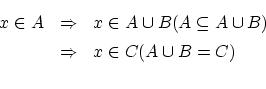
また
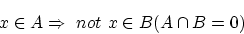
よって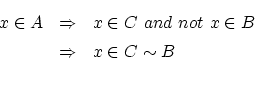
逆に,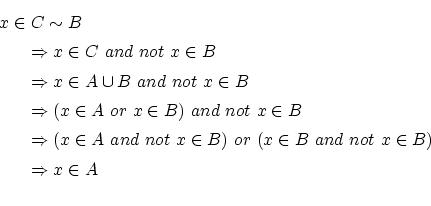
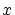 は任意にとったから
は任意にとったから
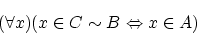
よって
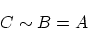
これは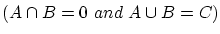 を仮定して得られたから
を仮定して得られたから
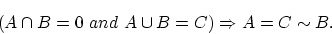
- (3)-II
-
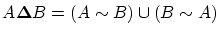 を対称差といいます.論理回路
をやった方は EX-OR(排他的論理和)に対応するものです.
(f)で
を対称差といいます.論理回路
をやった方は EX-OR(排他的論理和)に対応するものです.
(f)で
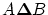 がどういうものかよくわかりますね.
この
がどういうものかよくわかりますね.
この 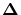 の挙動をみて,あれっと思いませんか?
の挙動をみて,あれっと思いませんか?
-
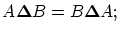
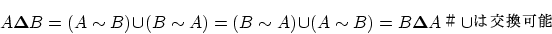
-
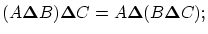
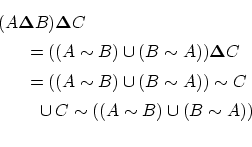
以後根気良く計算をすれば
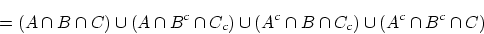
また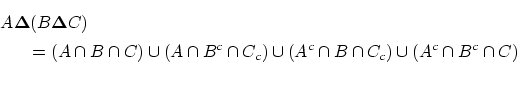
よって
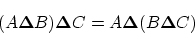
[別解] : 下の(f)
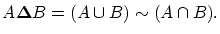 を用いて
を用いて
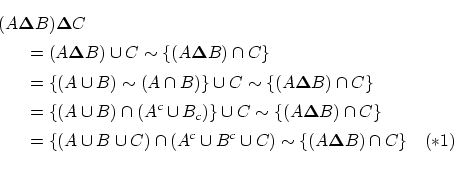
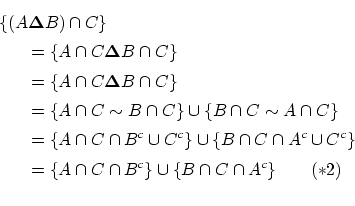
(*1)(*2)から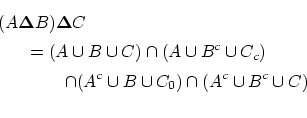
同様に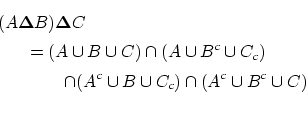
-
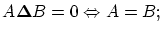
まず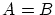 なら
なら
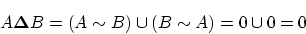
逆に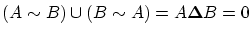 なら
なら
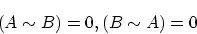
となるから より
より
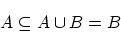
となり, 同様に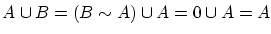 より
より
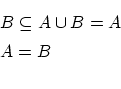
-
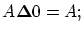
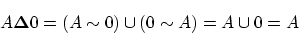
-
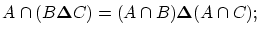
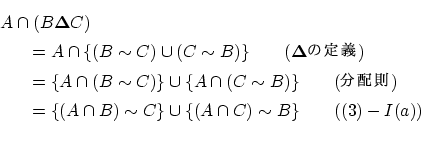
ここで(3)-I (d)より
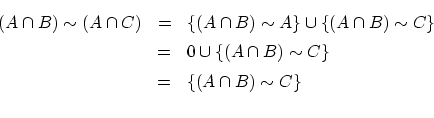
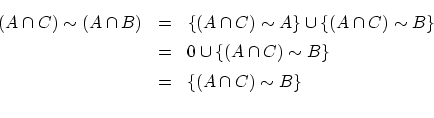
となるので, 結局
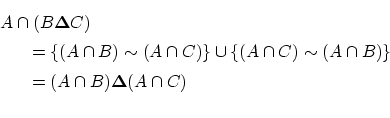
-
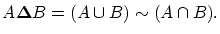
(3-I-(d))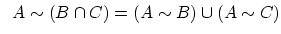 により
により
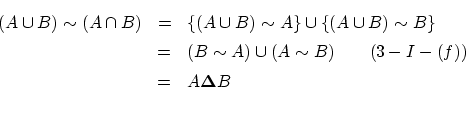
-