『系4 もし, ![]() が集合の体ならば,
が集合の体ならば,
![]() は
は ![]() 』
』
- [証明]
- 集合の体の定義と集合演算の規則によります。集合演算の規則は前節の演習でやったので全て既知とします.
-
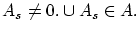 また,
また, 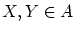 なら
なら
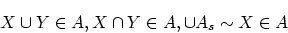
すなわち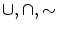 について閉じている.
について閉じている.
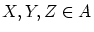 を任意にとると,
を任意にとると,
-
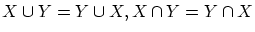 (交換律,交換法則)
(交換律,交換法則) -
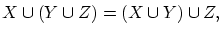
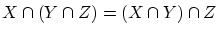 (結合律,結合法則)
(結合律,結合法則) -
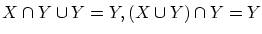 (吸収律,吸収法則)
(吸収律,吸収法則) -
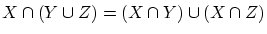
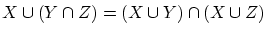 (分配律,分配法則)
(分配律,分配法則) -
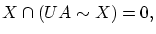
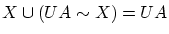 (補元律,補元法則,相補法則)
(補元律,補元法則,相補法則)
-
-
もし,
- [証明]
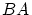 の定義から自明.
ただし、(2)(i)
の定義から自明.
ただし、(2)(i)  (v)の各式については,第1式と第2式の順序を逆にする.
(v)の各式については,第1式と第2式の順序を逆にする.
- [証明]
-
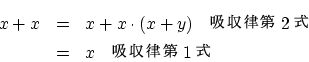





- [証明]
-
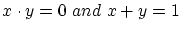 を仮定すると
を仮定すると


よって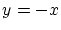
(証明終)
- [証明]
- まず.
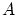 は空でないので
は空でないので 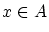 が少なくとも一つ存在する.
ここで0と1の働きをする要素0'と1'が在ったとしても
補元律より
が少なくとも一つ存在する.
ここで0と1の働きをする要素0'と1'が在ったとしても
補元律より
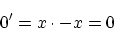
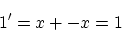
[証明終]
-
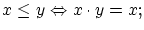
-
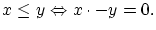
- [証明]
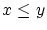 のとき
のとき 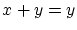 で,
で,

逆に、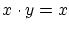 のとき
のとき
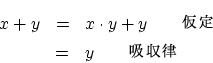
よって定義から
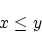
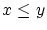 のとき
のとき 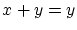 で,
で,

逆に,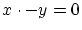 のとき,ドモルガン則と
のとき,ドモルガン則と 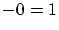 から
から

よって定義から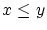
*(6)で使ったドモルガン則
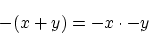
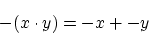
の証明は

よって,既に証明した補元の一意性から
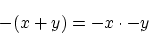
第2式も同様にできる.[証明終]
* -0=1については
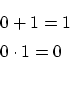
と補元の一意性による.
全く同様に -1=0
-1=0