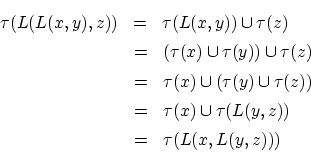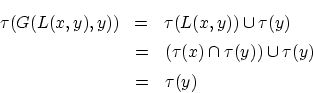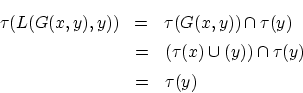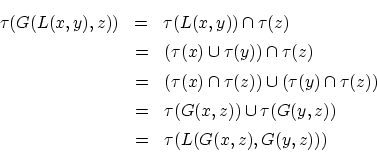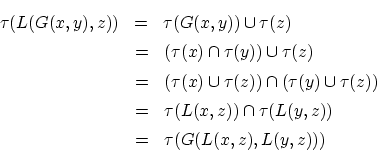ЄЌРЎЮЉЄЙЄыЄГЄШЄђЁЄОкЬРЄЗЄЪЄЕЄЄЁЅ
- [ОкЬР]
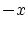 ЄЯ
ЄЯ 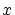 ЄЮЪфИЕЄРЄЋЄщФъЕСЄЫЄшЄъ
ЄЮЪфИЕЄРЄЋЄщФъЕСЄЫЄшЄъ
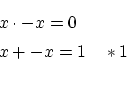
 ЄЯ
ЄЯ  ЄЮЪфИЕЄРЄЋЄщФъЕСЄЫЄшЄъ
ЄЮЪфИЕЄРЄЋЄщФъЕСЄЫЄшЄъ
ИђДЙЮЇЄЫЄшЄъ
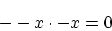
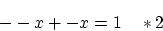
2СШЄЮМА*1,*2ЄЫЄшЄъЪфИЕЄЮАьАеРЄЋЄщ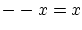
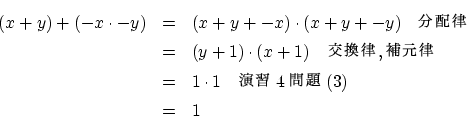

ЄшЄУЄЦ,ДћЄЫОкЬРЄЗЄПЪфИЕЄЮАьАеРЄЋЄщ
АЪИх,ИјЭ§,БщНЌ4ЄЮЗыВЬ,ЄЯУЧЄъЬЕЄЏЛШЄЄЄоЄЙ.СаТаЄЮИЖЭ§ЄЫЄшЄьЄа
ЄшЄУЄЦ,ЪфИЕЄЮАьАеРЄЋЄщ
-
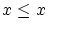 (ШПМЭЮЇ);
(ШПМЭЮЇ); -
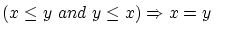 (ШПТаОЮЮЇ);
(ШПТаОЮЮЇ); -
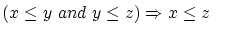 (ПфАмЮЇ);
(ПфАмЮЇ);
- [ОкЬР]
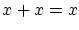 ЄЋЄщФъЕСЄЫЄшЄъ
ЄЋЄщФъЕСЄЫЄшЄъ 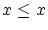
-
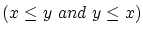
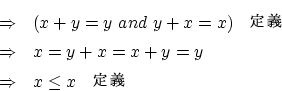
-
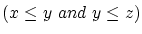
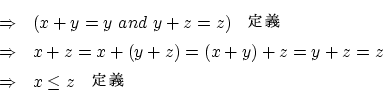
[ОкЬР]
-
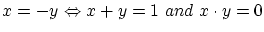 ЄЪЄщЄа,ЪфИЕЄЮАьАеТИКпЄЮЄГЄШЄЧЄЙЄЋЄщ
ЄЪЄщЄа,ЪфИЕЄЮАьАеТИКпЄЮЄГЄШЄЧЄЙЄЋЄщ
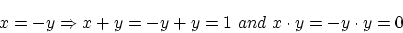
ЕеЄЫ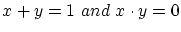 ЄЯАЪВМЄЮЄшЄІЄЫБщНЌ3ЄЧОкЬРКбЄпЄЧЄЙ.
ЄЯАЪВМЄЮЄшЄІЄЫБщНЌ3ЄЧОкЬРКбЄпЄЧЄЙ.
ЮуЄЈЄа
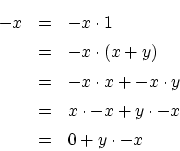
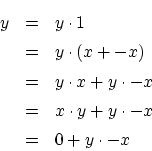
ЄшЄУЄЦ
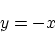
ЁЁЁЁ 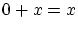 ЄЋЄщФъЕСЄЫЄшЄъ
ЄЋЄщФъЕСЄЫЄшЄъ 
 ЄЋЄщ ФъЕСЄЫЄшЄъ
ЄЋЄщ ФъЕСЄЫЄшЄъ 
-
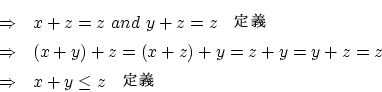
- (d-1)
-
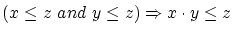
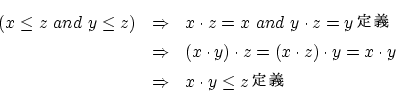
- (d-2)
-
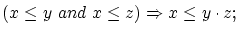
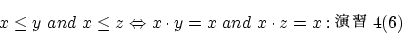
ЄЧЄЂЄыЄГЄШЄЋЄщ,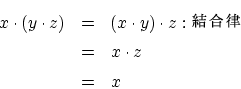
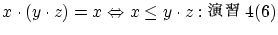
[ОкЬРНЊЄяЄъ]
-
[ОкЬР]
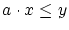 ЄЪЄщФъЕСЄЫЄшЄъ
ЄЪЄщФъЕСЄЫЄшЄъ 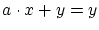 ЄЧ
ЄЧ
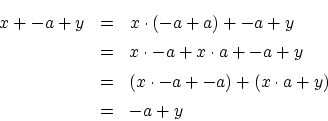
ЄшЄУЄЦ
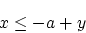
ЕеЄЫ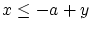 ЄЪЄщФъЕСЄЫЄшЄъ
ЄЪЄщФъЕСЄЫЄшЄъ
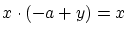 ЄЧ
ЄЧ
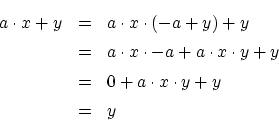
ЄшЄУЄЦ
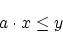

ОхЄЧЭбЄЄЄПЅЩЁІЅтЅыЅЌЅѓТЇЄЮАьШЬВН
ЄЫЄФЄЦЄЯ
- [ОкЬР]
- ПєГиХЊЕЂЧМЫЁЄђЛШЄІЄШ
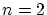 ЄЫЄФЄЄЄЦЄЯРЎЮЉ.(ДћЄЫОкЬРКбЄп)
ЄЫЄФЄЄЄЦЄЯРЎЮЉ.(ДћЄЫОкЬРКбЄп)
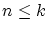 ЄЫЄФЄЄЄЦРЎЮЉЄФЄШВОФъЄЗЄЦ
ЄЫЄФЄЄЄЦРЎЮЉЄФЄШВОФъЄЗЄЦ

ЄшЄУЄЦ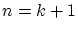 ЄЮОьЙчЄтРЎЮЉ.
ЄЮОьЙчЄтРЎЮЉ.
ЄоЄПСаТаИЖЭ§ЄЫЄшЄъ
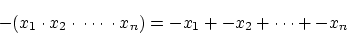
[ОкЬРНЊ]
ЄШЄЊЄЄоЄЙ. ЧЄАеЄЮ
- ЧЄАеЄЮ
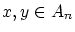 ЄЫЄФЄЄЄЦ,
ЄЫЄФЄЄЄЦ,
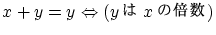 ЄђОкЬРЄЗЄЪЄЕЄЄ.
ЄђОкЬРЄЗЄЪЄЕЄЄ.
- [ОкЬР]
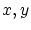 ЄЮКЧОЎИјЧмПєЄђ
ЄЮКЧОЎИјЧмПєЄђ 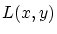 ЄЧЩНЄЙЄГЄШЄЫЄЙЄыЄШ
ЄЧЩНЄЙЄГЄШЄЫЄЙЄыЄШ
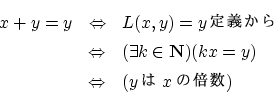
[ОкЬРНЊ]
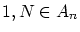 ЄЧЄЂЄыЄГЄШЄђГЮЧЇЄЗЄЪЄЕЄЄ.
ЄЧЄЂЄыЄГЄШЄђГЮЧЇЄЗЄЪЄЕЄЄ.
- [ОкЬР]
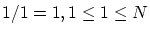 ЄцЄЈ
ЄцЄЈ 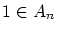
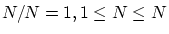 ЄцЄЈ
ЄцЄЈ 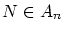
[ОкЬРНЊ]
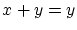 Єђ,
Єђ, 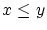 ЄШНёЄЏЄГЄШЄЫЄЙЄы.
ЧЄАеЄЮ
ЄШНёЄЏЄГЄШЄЫЄЙЄы.
ЧЄАеЄЮ 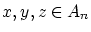 ЄЫЄФЄЄЄЦ
ЄЫЄФЄЄЄЦ
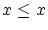 (ШПМЭЮЇ);
(ШПМЭЮЇ);-
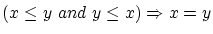 (ШПТаОЮЮЇ);
(ШПТаОЮЮЇ); -
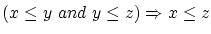 (ПфАмЮЇ)
(ПфАмЮЇ)
- [ОкЬР]
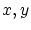 ЄЮКЧОЎИјЧмПєЄђ
ЄЮКЧОЎИјЧмПєЄђ 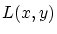 ЄЧЩНЄЙЄГЄШЄЫЄЙЄыЄШ
ЄЧЩНЄЙЄГЄШЄЫЄЙЄыЄШ
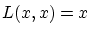 ЄцЄЈ
ЄцЄЈ
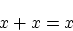
ЄшЄУЄЦ
-
 ЄШЄЙЄыЄШ
ЄШЄЙЄыЄШ
ЄГЄГЄЧ
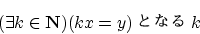
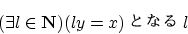
ЄђСЊЄжЄШ,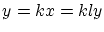 ЄЋЄщ
ЄЋЄщ 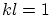 ЄшЄУЄЦ
ЄшЄУЄЦ
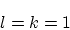
ЁЁЁЁЁЁЄшЄУЄЦ
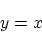
-
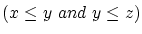 ЄШЄЙЄыЄШ
ЄШЄЙЄыЄШ
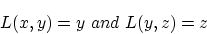
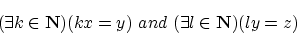
ЁЁЁЁЁЁЄГЄГЄЧ
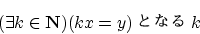
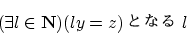
ЄђСЊЄжЄШ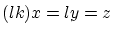 ЄшЄУЄЦ
ЄшЄУЄЦ
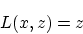
ЄцЄЈЄЫ
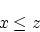
- ЧЄАеЄЮ
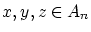 ЄЫЄФЄЄЄЦ,
ЄЫЄФЄЄЄЦ,
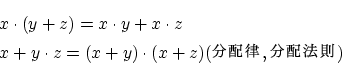
- [ОкЬР]
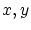 ЄЮКЧОЎИјЧмПєЄђ
ЄЮКЧОЎИјЧмПєЄђ 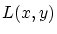 ЄЧ,КЧТчИјЬѓПєЄШ
ЄЧ,КЧТчИјЬѓПєЄШ 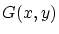 ЄЧЩНЄЙЄГЄШ
ЄЫЄЙЄыЄШ
ЄЧЩНЄЙЄГЄШ
ЄЫЄЙЄыЄШ

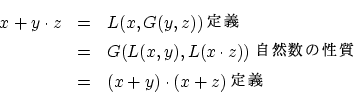
-
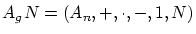 ЄЯЅжЁМЅыТхПєЄЧЄЂЄыЄГЄШЄђ
ОкЬРЄЗЄЪЄЕЄЄ.
ЄЯЅжЁМЅыТхПєЄЧЄЂЄыЄГЄШЄђ
ОкЬРЄЗЄЪЄЕЄЄ.
- [ОкЬР]
-
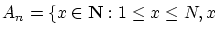 ЄЯ
ЄЯ 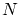 ЄђГфЄъРкЄы
(ЄФЄоЄъ,
ЄђГфЄъРкЄы
(ЄФЄоЄъ, 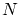 ЄЯ
ЄЯ 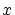 ЄЮЧмПє)
ЄЮЧмПє) 
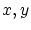 ЄЮКЧОЎИјЧмПєЄђ
ЄЮКЧОЎИјЧмПєЄђ 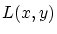 ЄЧ,КЧТчИјЬѓПєЄШ
ЄЧ,КЧТчИјЬѓПєЄШ 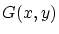 ЄЧЩНЄЙЄГЄШ
ЄЫЄЙЄы.
ЄЧЩНЄЙЄГЄШ
ЄЫЄЙЄы.
- (1)
- (b)ЄЋЄщ
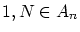 ЄЧ
ЄЧ 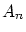 ЄЯЖѕЄЧЄЪЄЄНИЙчЄЧЄЂЄы.
ЄЯЖѕЄЧЄЪЄЄНИЙчЄЧЄЂЄы.
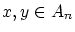 ЄЫЄФЄЄЄЦ
ЄЫЄФЄЄЄЦ
 ЄШ
ЄЙЄыЄШ
ЄШ
ЄЙЄыЄШ
 ЄЋЄщ
ЄЋЄщ
ЄГЄЮЄшЄІЄЪ
 ЄђСЊЄйЄа
ЄђСЊЄйЄа 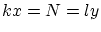 ЄЙЄЪЄяЄС,
ЄЙЄЪЄяЄС, 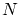 ЄЯ
ЄЯ 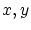 ЄЮИјЧмПє. ЄшЄУЄЦКЧОЎИјЧмПє
ЄЮИјЧмПє. ЄшЄУЄЦКЧОЎИјЧмПє 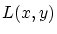 ЄЯ
ЄЯ 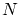 Єђ
ГфЄъРкЄы.
Єђ
ГфЄъРкЄы.
ЄоЄП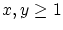 ЄЋЄщ
ЄЋЄщ 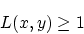
ЄшЄУЄЦ
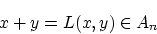
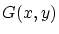 ЄЯ
ЄЯ 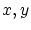 ЄђГфЄъРкЄъ,
ЄђГфЄъРкЄъ, 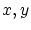 ЄЯ
ЄЯ 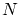 ЄђГфЄъРкЄыЄЋЄщ
ЄђГфЄъРкЄыЄЋЄщ
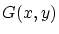 ЄЯНОЄУЄЦ
ЄЯНОЄУЄЦ 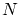 ЄђГфЄъРкЄы. ЄоЄП
ЄђГфЄъРкЄы. ЄоЄП 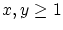 ЄЋЄщ
ЄЋЄщ
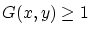 ЄшЄУЄЦ
ЄшЄУЄЦ
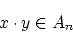
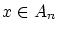 ЄЪЄщ
ЄЪЄщ
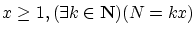 ЄЧ
ЄНЄЮЄшЄІЄЪ
ЄЧ
ЄНЄЮЄшЄІЄЪ 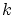 ЄђЄШЄьЄа
ЄђЄШЄьЄа 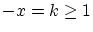 ЄЧ,
ЄЧ, 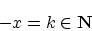
ЄшЄУЄЦ ЄЯ
ЄЯ  ЄЫЄФЄЄЄЦЪФЄИЄЦЄЄЄы;
ЄЫЄФЄЄЄЦЪФЄИЄЦЄЄЄы;
- (2)
- ЧЄАеЄЮ
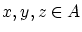 ЄЫЄФЄЄЄЦЁЇ
ЄЫЄФЄЄЄЦЁЇ
- (њР)
-
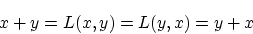
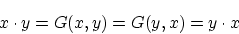
- (њС)
-
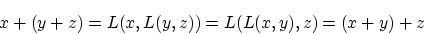
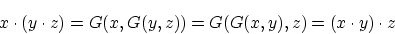
- (њТ)
-
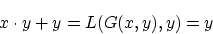
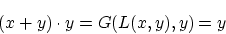
- (њУ)
- (d)ЄшЄъ
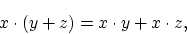
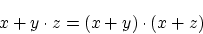
- (њФ)
- ЄЩЄѓЄЪСЧПє
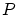 ЄЫЄФЄЄЄЦЄт,
ЄЫЄФЄЄЄЦЄт, 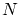 ЄЯ
ЄЯ 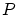 ЄЮ2ОшЄЧГфЄъРкЄьЄЪЄЄ
ЄЋЄщ
ЄЮ2ОшЄЧГфЄъРкЄьЄЪЄЄ
ЄЋЄщ
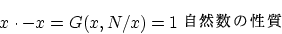
ЄоЄП,