


: 演習15
: 演習の解答
: 演習13
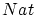 を自然数全体の集合とします.
を自然数全体の集合とします. 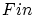 を
を 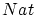 の有限部分集合の全体と
します.
の有限部分集合の全体と
します. 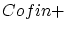 を
を 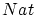 の部分集合
の部分集合 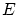 で,
で, 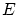 または
または
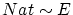 が有限になるもの全体の集合とします. さらに,
が有限になるもの全体の集合とします. さらに, 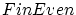 を
を
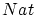 の有限部分集合で偶数のみからなる集合全体の集合とします.
このとき,半順序集合
の有限部分集合で偶数のみからなる集合全体の集合とします.
このとき,半順序集合
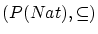 とその部分半順序集合
とその部分半順序集合
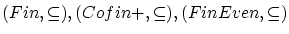 を考えます.
を考えます.
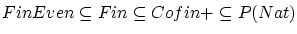 は明らかです.
は明らかです.
このとき,
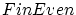 は
は
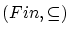 では上界を持たない.
では上界を持たない.
- [証明]
- 背理法によります.
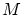 を
を 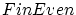 の
の
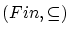 での上界と
すると,
任意の
での上界と
すると,
任意の 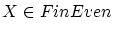 について,
について,
任意 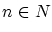 について偶数
について偶数
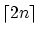 1個だけからなる集合
1個だけからなる集合
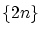 は
は
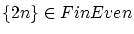 で,これから
で,これから
これは, 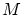 が有限集合である (
が有限集合である ( 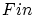 の元である)ことに反します.
の元である)ことに反します.
[証明終]
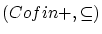 では無限個の上界を持つことを確かめなさい.
では無限個の上界を持つことを確かめなさい.
- [証明]
- 例えば任意の
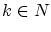 について,
について,
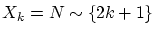 とおくと
とおくと
ゆえ,
で,
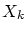 は奇数
は奇数 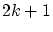 を1個だけ
を1個だけ 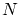 から取り除いた,
から取り除いた, 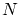 の部分集合ですから,
の部分集合ですから,
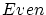 を偶数全体の集合とすと,
を偶数全体の集合とすと,
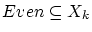 で
で
よって, 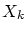 は
は 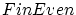 の
の 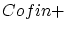 の上界で,
の上界で, 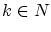 を
を 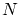 全体で
動かせば,このような
全体で
動かせば,このような 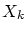 は無限個.
は無限個.
[証明終]
- また,
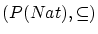 では,偶数全体の集合が
では,偶数全体の集合が 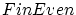 の
上限になっていることを確かめなさい.
の
上限になっていることを確かめなさい.
- [証明]
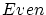 を偶数全体の集合とすると,
を偶数全体の集合とすると,
ゆえ, 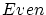 は
は 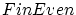 の
の
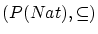 での上界
での上界
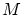 を
を 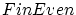 の任意の上界とすると,
の任意の上界とすると,
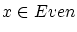 を任意にとれば,
を任意にとれば, 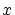 は偶数で,
は偶数で,
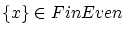 で
で
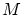 は
は 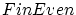 の上界だから
の上界だから
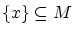 よって
よって 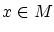
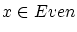 を任意にとったから
を任意にとったから
よって
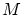 は任意にとったから
は任意にとったから 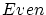 は上界の最小元.すなわち上限.
は上界の最小元.すなわち上限.
[証明終]



: 演習15
: 演習の解答
: 演習13
Yasunari SHIDAMA
![]() を自然数全体の集合とします.
を自然数全体の集合とします. ![]() を
を ![]() の有限部分集合の全体と
します.
の有限部分集合の全体と
します. ![]() を
を ![]() の部分集合
の部分集合 ![]() で,
で, ![]() または
または
![]() が有限になるもの全体の集合とします. さらに,
が有限になるもの全体の集合とします. さらに, ![]() を
を
![]() の有限部分集合で偶数のみからなる集合全体の集合とします.
このとき,半順序集合
の有限部分集合で偶数のみからなる集合全体の集合とします.
このとき,半順序集合
![]() とその部分半順序集合
とその部分半順序集合
![]() を考えます.
を考えます.
![]() は明らかです.
は明らかです.
![]() では無限個の上界を持つことを確かめなさい.
では無限個の上界を持つことを確かめなさい.