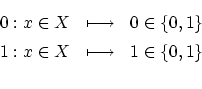

ただし,上の定義式の右辺の
![]() についての演算
についての演算
![]() はブール代数
はブール代数
![]() の演算です.
の演算です.
これは ![]() が何れも
が何れも ![]() 上で定義され,0か1の値しか取らない関数であるこ
とと,(0)で述べたように
上で定義され,0か1の値しか取らない関数であるこ
とと,(0)で述べたように
![]() がブール代数である
ことを用いて根気良くチェックすればできます.
がブール代数である
ことを用いて根気良くチェックすればできます.
以下,各 ![]() に対する
に対する
![]() についての演算
についての演算
![]() は(0)のブール代数
は(0)のブール代数
![]() の演算で,
交換律,結合律,吸収律,補元律その他は断りなく使います.
の演算で,
交換律,結合律,吸収律,補元律その他は断りなく使います.
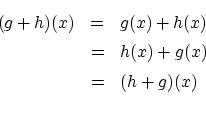
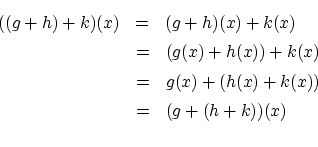
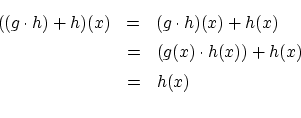
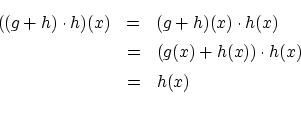
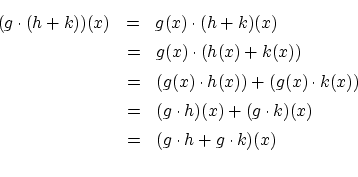
![]() を任意とると
を任意とると
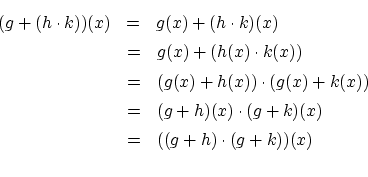
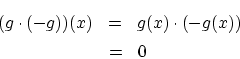
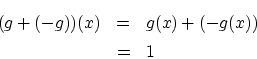
よって
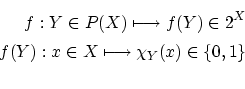
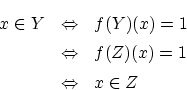
![]() のとき
のとき
![]() の特性関数については
の特性関数については
![]() のとき
のとき
また,
![]() ゆえ
ゆえ
![]() から
から
結局,どちらの場合でも
![]() を任意にとると
を任意にとると
![]() のとき
のとき
![]() を任意にとると
を任意にとると
![]() のとき
のとき
(命題)
ブール代数の同型写像の逆写像は,またブール代数の同型写像である.
(命題終わり)
任意の ![]() について,
について,
![]() がいえるから,上の式は
がいえるから,上の式は
同様にして,任意の ![]() について,
について,
![]() ですから,
ですから, ![]() が
準同型写像であることから,
が
準同型写像であることから,
上と同様に考えて,