集合の体(field of sets)
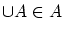
- 任意の
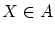 について,
について,
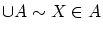
- 任意の
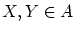 について,
について,
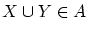 .
またこのとき,
.
またこのとき,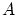 を
を 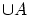 の部分集合の体という.
の部分集合の体という.
皆さんは,意識的にあるいは無意識のうちにブール代数にはすでに何らかの形で出会っていると思います。
論理回路を通じて,集合の演算を通じて,あるいは命題論理等を通じてです。
しかしながら,ブール代数を数学における代数学としてきちんと習ったことはないのではないでしょうか.
今回のセミナーの目的は,そこにあります。
つまり,ブール代数を数学における代数学としてきちんと理論的
に学ぶということです(数理論理学者の目を通じてということですが).私はブール代数を奥が深い数学の
一分野だと思っています。
ブール代数における代数構造は命題論理と親密な関係にあります。
また,それには応用があります(論理回路等).
ブール代数は初等集合論から最も簡単に動機付けできるでしょう.
ここで,若干の記号の説明と約束をします。
まず記号のお約束.![]() を集合とするとき,
を集合とするとき,
「![]() 」という記号は,公理的集合論の方からの記号法です。
」という記号は,公理的集合論の方からの記号法です。
公理的集合論は,広い意味での数理論理学(Logic)の一部分で等号を含む
1階古典述語論理に基づいて公理的に集合論を展開する学問です。
非常に高度に発達している分野です。
大雑把にいって,その根底の考え方の一つは,数学的対象の全てを集合として考える,ということです。
![]() の説明に戻ります。
の説明に戻ります。
つまり, ![]() を集合とすると,
を集合とすると, ![]() の和(あるいは和集合)
の和(あるいは和集合) ![]() は
は ![]() の要素の要素全体からなる集合です。
の要素の要素全体からなる集合です。
集合の体![]() とは,
とは, ![]() に関する補集合と合併をとる演算に関して閉じている集合であるといえます。
に関する補集合と合併をとる演算に関して閉じている集合であるといえます。
すこし表現を変えれば,集合の体 ![]() とは,
とは, ![]() の要素の要素全体からなる集合
の要素の要素全体からなる集合 ![]() を全体と考えて,その部分集合につい
ての(
を全体と考えて,その部分集合につい
ての( ![]() に関する)補集合と合併をとる演算に関して閉じている集合です。
に関する)補集合と合併をとる演算に関して閉じている集合です。
「閉じている」について説明します。
まず,例で言った方が速いでしょう.
![]() を整数全体の集合とします。
を整数全体の集合とします。 ![]() の
任意の要素
の
任意の要素 ![]() について,
について, ![]() がまた
がまた ![]() の要素となるとき,
の要素となるとき, ![]() は加法+について(に関して)閉じているといいます。
は加法+について(に関して)閉じているといいます。
![]() を正の整数全体の集合とします。
を正の整数全体の集合とします。 ![]() の任意の要素
の任意の要素 ![]() について,
について, ![]() は必ずしも
は必ずしも ![]() の要素とはなりません.
の要素とはなりません.
例えば ![]() ですから.
ですから.
![]() は減法−について閉じていません.ところが,
は減法−について閉じていません.ところが,![]() は当然,減法−について閉じています。
は当然,減法−について閉じています。
一般の場合は,
[一般の場合]
一般に,集合 ![]() について,
について,![]() を直積
を直積 ![]() から
から ![]() への写像とし,
への写像とし,
[一般の場合の説明終わり]
命題2で ![]() は空集合を表します。
は空集合を表します。
つまり,集合の体 ![]() は空集合を要素に持ち,演算
は空集合を要素に持ち,演算 ![]() について閉じている集合ということです。
について閉じている集合ということです。
それではさっそく演習です。