-
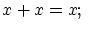 (べき等律)
(べき等律) -
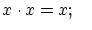 (べき等律)
(べき等律) -
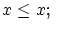 (反射律)
(反射律) -
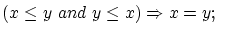 (反対称律)
(反対称律) -
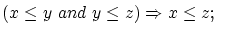 (推移律)
(推移律) -
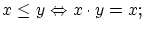
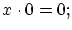

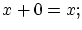
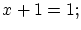
-
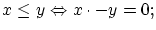
-
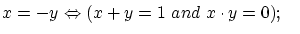 (補元の一意性)
(補元の一意性) -
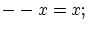 (二重否定の法則)
(二重否定の法則) -
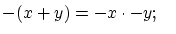 (ド・モルガンの法則)
(ド・モルガンの法則) -
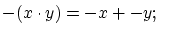 (ド・モルガンの法則)
(ド・モルガンの法則) -
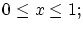
-
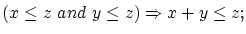
-
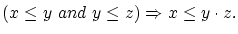



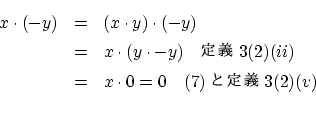




[命題6(その1)の証明終わり]
もう少し,ブール代数の初等的な性質を見てみましょう.
(命題6(その2)終わり)
少し,ウォーミングアップをしましょう.
さて,ブール代数は束論(lattice theory)の方から特徴付けできます。
つまり,ブール代数は相補的な分配束として定義することができます。
それについて少し触れておきましょう.少し長い準備が必要です。
この節はその準備で終わってしまいます。
次節で,
ブール代数を相補的な分配束として定義しましょう.
まず,束を定義したいのですが,そのために半順序の概念が必要です。
(順序に関して,定義が分散すると嫌なので,下でかなりまとまって書いてしまいます。
そのため,順序について慣れていない方はつらいと思います。
しかし,これ以後(できれば次回も),逐次演習など入れていきますのでだんだんに慣れていってください.)
半順序集合((partially ordered set,略してよく poset (ポーセットと読む)といわれる) とは,
集合 ![]() と次の (1)
と次の (1) ![]() (3)を満足する
(3)を満足する ![]() 上の2項関係
上の2項関係 ![]() の組
の組
![]() のことです: 任意の
のことです: 任意の ![]() について,
について,
このとき, ![]() は順序関係 (order relation),特に(
は順序関係 (order relation),特に( ![]() 上の)(半)順序((partial) order)といいます。
上の)(半)順序((partial) order)といいます。
![]() が空集合のときも定義できるものとします。
が空集合のときも定義できるものとします。
また,明らかに混乱が起きない場合,( ![]() )を単に
)を単に ![]() と書きます。
と書きます。
![]() を集合を要素とする集合とすると,集合間の包含関係
を集合を要素とする集合とすると,集合間の包含関係 ![]() は明らかに順序関係となり,
は明らかに順序関係となり,
![]() は半順序集合です。
は半順序集合です。
また, ![]() を
を ![]() とも書くことにします。
とも書くことにします。
この定義から,命題6(その1)によって,ブール代数 ![]() で定義された
で定義された ![]() に関して,
に関して, ![]() は半順序集合になります。
は半順序集合になります。
任意の集合 ![]() について,
について,
![]() も半順序集合です。
も半順序集合です。
![]() を半順序集合とします。
を半順序集合とします。
![]() を
を ![]() の部分集合とします。
の部分集合とします。
このとき,
![]() を
を ![]() を
を ![]() 上で考えたものとすれば,
上で考えたものとすれば, ![]() は半順序集合になります。
は半順序集合になります。
この ![]() を単に,
を単に, ![]() で表すことにします。
で表すことにします。
![]() は
は
![]() の部分半順序集合といいます。
の部分半順序集合といいます。
![]() をブール代数
をブール代数 ![]() の部分宇宙とします。
の部分宇宙とします。
![]() で定義された
で定義された ![]() に関して,
に関して, ![]() は
は ![]() の部分半順序集合になります。
の部分半順序集合になります。
![]() を半順序集合とします。
を半順序集合とします。
![]() の要素
の要素 ![]() は全ての
は全ての ![]() について,
について, ![]() となるとき,最大元といいます。
となるとき,最大元といいます。
同様に, ![]() の要素
の要素 ![]() は全ての
は全ての
![]() について,
について, ![]() となるとき,最小元といいます。
となるとき,最小元といいます。
![]() は常に最大元または最小元を持つとは限りません.
は常に最大元または最小元を持つとは限りません.
![]() の最大元が存在するときはそれを1で,最小元が存在するときはそれを0で表します。
の最大元が存在するときはそれを1で,最小元が存在するときはそれを0で表します。
半順序集合 ![]() の,元
の,元 ![]() は,
は,
![]() がいえるとき,比較可能であるといいます。
がいえるとき,比較可能であるといいます。
![]() の部分集合
の部分集合 ![]() は,
は, ![]() の全ての2つの元が比較可能なとき,連鎖(または,鎖)(chain) といいます。
の全ての2つの元が比較可能なとき,連鎖(または,鎖)(chain) といいます。
![]() 自身が連鎖のとき,
自身が連鎖のとき,
![]() を全順序集合 (totally ordered set), あるいは,線形順序集合(linearly ordered set)といいます。
を全順序集合 (totally ordered set), あるいは,線形順序集合(linearly ordered set)といいます。
そのとき, ![]() は (
は ( ![]() 上の) 全順序(total order),あるいは線形順序(linear order)といいます。
上の) 全順序(total order),あるいは線形順序(linear order)といいます。
任意の要素 ![]() について,
について, ![]() または
または ![]() のいずれかが成り立つとき,
のいずれかが成り立つとき, ![]() を全順序集合であるというわけです。
を全順序集合であるというわけです。
「任意の要素 ![]() について,
について, ![]() または
または ![]() のいずれかが成り立つ」というところは,
「任意の要素
のいずれかが成り立つ」というところは,
「任意の要素 ![]() について,
について,
![]() 」といってもかまいません.
」といってもかまいません.
ここで, ![]() は
は
![]() によって定義されます。
によって定義されます。
上と同様, ![]() を
を ![]() とも書くことにします。
とも書くことにします。
実数全体の集合,有理数全体の集合,整数全体の集合などは,普通の順序で考えて全順序集合です。
![]() を半順序集合
を半順序集合 ![]() の部分集合とします。
の部分集合とします。
![]() の要素
の要素 ![]() は,全ての
は,全ての
![]() について,
について,
![]() を満足するとき,
を満足するとき, ![]() の上界(下界)と呼ばれ,
の上界(下界)と呼ばれ,
![]() と書きます。
と書きます。
![]() に上界(下界)が存在するとき,
に上界(下界)が存在するとき, ![]() は上に(下に)有界であるといいます。
は上に(下に)有界であるといいます。
![]() は上界を持たないこともあるし,
無限個の上界を持つこともあります。
は上界を持たないこともあるし,
無限個の上界を持つこともあります。
これは下界についても同様です。
特に, ![]() が最小の上界(最大の下界)であるとき,
が最小の上界(最大の下界)であるとき, ![]() の上限(下限)といいます。
の上限(下限)といいます。
それらの英語は,上界(upper bound),
下界(lower bound),上限(supremum),下限(infinimum) です。
![]() の上限(下限)であるとき,
の上限(下限)であるとき,
![]() (
( ![]() は
は ![]() の大文字)で表します。
の大文字)で表します。
![]() を,
を,
![]() や
や
![]() で表すことも多いです。
で表すことも多いです。
半順序集合 ![]() の要素(元)
の要素(元) ![]() が,
が, ![]() となる
となる ![]() が存在しないとき,
が存在しないとき,![]() の極大元といいます。
の極大元といいます。
同様に, ![]() の要素(元)
の要素(元) ![]() が
が ![]() となる
となる ![]() が存在しないとき,
が存在しないとき, ![]() の極小元といいます。
の極小元といいます。
極大元(極小元)はないこともありますし,1つあるいは複数個あることもあります。
![]() が最大元(最小元)を持つとき,それはただ一つの極大元(極小元)となります。
が最大元(最小元)を持つとき,それはただ一つの極大元(極小元)となります。
ちょっと寄り道ですが,半順序集合 ![]() が帰納的順序集合
(inductively ordered set) であるとは,
が帰納的順序集合
(inductively ordered set) であるとは, ![]() であって,
であって, ![]() の任意の空でない全順序部分集合(=連鎖)が
上に有界である(上界が存在する)であることをいいます。
の任意の空でない全順序部分集合(=連鎖)が
上に有界である(上界が存在する)であることをいいます。
ここで,数学の証明に良く用いる有名な ![]() (ツォルン) の補題を紹介しましょう.それは,
「半順序集合
(ツォルン) の補題を紹介しましょう.それは,
「半順序集合 ![]() が帰納的順序集合ならば,
が帰納的順序集合ならば, ![]() は極大元を持つ.」
です。
は極大元を持つ.」
です。
これは集合論の選択公理と同値になります。
選択公理とは,集合論の悩ましい(?)
公理で,「2つずつ互いに素な空でない集合からなる集合 ![]() が与えられているとき,
次の条件を満たす集合
が与えられているとき,
次の条件を満たす集合 ![]() が存在する:任意の
が存在する:任意の ![]() について,
について,
![]() となる集合
となる集合 ![]() が存在する.」
というものです。
が存在する.」
というものです。
選択公理には色々なバージョンがあります。
選択公理は証明するときの良い道具になるのですが,悩ましいというのは,これから,常識外のことが導き出せるからです。
たとえば,球を適当に分割してまた寄せ集めると,元の球と全く同じ球を2つ作れるという,バナッハ・
タルスキーのパラドックスが選択公理から証明できます。
これについては,
砂田利一著「バナッハ・タルスキーのパラドックス」岩波書店 1997年
という本があります。
砂田さんは数学者として著名な方です。
たしか,志賀浩二著「無限からの光芒ポーランド学派の数学者達」日本評論社 1988年
にも,その記述があったように記憶しています。
はっきり記憶していませんが.志賀さんも数学者として著名な方です。
上の2冊とも昔,書店でパラパラと見ただけなので本当に推薦すべき書物かどうかはわかりません.
著名な方が書いておられるので大丈夫だとは思います。
洋書でも,バナッハ・タルスキーのパラドックスのみについて書かれたものを見たことがあります。
Banach-Tarski Pradox というタイトルだったかな.忘れました.
選択公理については,(真打登場!) 田中尚夫さんの, 田中尚夫著「選択公理と数学(増補版)」遊星社 1999年
に詳しい記述があります。
また,選択公理のみを扱った数理論理学の専門書 (洋書)
(The Axiom of Choice)が North-Holland社から2冊出ています。
田中さんの本はまたしてもお薦めです。
我々のブール代数とも関係があります。
機会があれば見てみてください.(田中さんの本にもバナッハ・タルスキーのパラドックスが,
今述べたものとはすこし異なるかたちで載っています。 )
このセミナーでも,近い将来,ツォルンの補題を用いて重要な定理を証明します。
さて,寄り道から本道に戻りましょう.
半順序集合 ![]() において,任意の2元
において,任意の2元 ![]() について,
集合
について,
集合 ![]() の上限および下限が (
の上限および下限が ( ![]() の中で)存在するとき,
の中で)存在するとき, ![]() を束(lattice)といいます。
を束(lattice)といいます。
空集合0,あるいはただ一つの要素からなる半順序集合もそれぞれ束をなします。
特に後者を単位束といいます。
![]() の上限,下限をそれぞれ,
の上限,下限をそれぞれ,
![]() と表します。
と表します。
+と ![]() の替わりに,それぞれ,
の替わりに,それぞれ, ![]() と
と ![]() とか,
とか, ![]() と
と ![]() を使うことも多いです。
を使うことも多いです。
束に関しても,双対の原理が成り立ちます。
(注: ![]() の双対命題は,
の双対命題は, ![]() です。 )
です。 )
任意の集合 ![]() について,
について,
![]() は束になります。
は束になります。