: 分岐限定法
: 整数計画法
: 整数計画法
第1章では,線形計画法の説明で典型的な問題として以下のような問題を例示しました。制約条件
のもとで,関数
を最大化する問題でした。
ここで,特に変数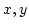 が整数値しか取り得ないという条件を付加します。
が整数値しか取り得ないという条件を付加します。
| |
|
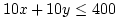 |
(17) |
| |
|
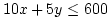 |
(18) |
| |
|
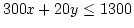 |
(19) |
| |
|
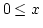 |
(20) |
| |
|
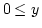 |
(21) |
| |
|
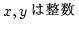 |
(22) |
のもとで,関数
を最大化する。このような問題を整数計画問題と言います。
一見すると,
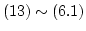 の問題を解き、解の
の問題を解き、解の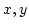 の値を四捨五入などすれば
の値を四捨五入などすれば
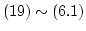 の解が得られるように思われるかもしれませんが,そう簡単にはいきません。
の解が得られるように思われるかもしれませんが,そう簡単にはいきません。
変数が整数という制約が加わると,難しくなります。
実際,整数値という制約のない問題
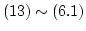 の解は,
の解は,
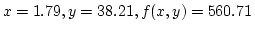 ですが,問題
ですが,問題
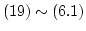 では,
では,
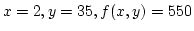 です。
です。
それぞれ重さが,
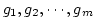 で,値段が
で,値段が
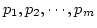 の
の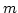 個の品物があり,それを,最大
個の品物があり,それを,最大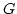 まで入れることが出きる容器に詰めるとして,売上が最大になる
ような詰め方は? という問題を定式化すると
まで入れることが出きる容器に詰めるとして,売上が最大になる
ような詰め方は? という問題を定式化すると
のもとで,
を最大にする。
ただし,変数
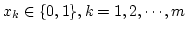
を表す。という問題になります。これはナップサック問題と呼ばれています。



: 分岐限定法
: 整数計画法
: 整数計画法
Yasunari SHIDAMA
![]() で,値段が
で,値段が
![]() の
の![]() 個の品物があり,それを,最大
個の品物があり,それを,最大![]() まで入れることが出きる容器に詰めるとして,売上が最大になる
ような詰め方は? という問題を定式化すると
まで入れることが出きる容器に詰めるとして,売上が最大になる
ような詰め方は? という問題を定式化すると