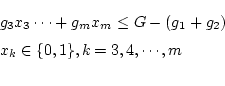: 変分問題(等周問題)
: 整数計画法
: 整数計画法
このような問題について,解法は種々考案されていますが,ネットワークの最適化
で述べた「分岐限定法」を適用することもできます。
「分岐限定法」を、この問題に適用するように書き直すと
最小化問題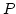 が与えられたとして:
が与えられたとして:
- (1)
-
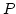 から,部分問題の集合
から,部分問題の集合
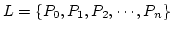 を作り,
を作り,
初期解を適当に選択してその値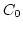 を求める。
を求める。
以下の手続きを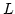 の元
の元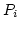 の全てについて行う
の全てについて行う
- (2)
- 最小問題
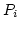 の解の上限値
の解の上限値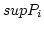 を求め,
を求め,
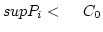 なら
なら
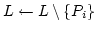
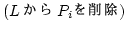
- (3)
- 最小問題
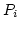 の解
の解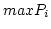 を求め
を求め
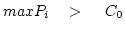 なら
なら
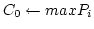 とする
とする
となります。部分問題の造り方は,詰める品物のいくつかを固定して,他の品物を詰めるかどうかの問題にするというものです。
制約条件
のもとで,
を最大にするのですから,例えば,品物1,2は必ず詰めるとして,
すなわち,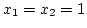 とおき,部分問題として
とおき,部分問題として
のもとで,
を最大化するというものです。



: 変分問題(等周問題)
: 整数計画法
: 整数計画法
Yasunari SHIDAMA
![]() が与えられたとして:
が与えられたとして: