


: 陰関数定理とラグランジュ乗数
: optimization
: 変分問題(等周問題)
「平面上の2点を結ぶ線分のうち長さが最小のものを求めよ」
簡単のため2点の座標を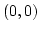 と
と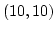 とてしておきます。
とてしておきます。
この2点を結ぶ線分を考えます。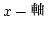 の0から10までを
の0から10までを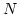 等分して
等分して
-
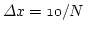
-
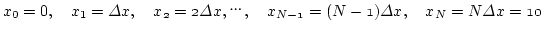
とし,
それに対応した線分上の点を
とします。
この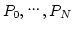 を結ぶ折れ線で問題の線分を近似します。
を結ぶ折れ線で問題の線分を近似します。
折れ線の線分の長さはピタゴラスの定理を使って
です。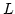 が最小になるように
が最小になるように
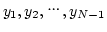 を求めればいいわけです。
を求めればいいわけです。



: 陰関数定理とラグランジュ乗数
: optimization
: 変分問題(等周問題)
Yasunari SHIDAMA
![]() と
と![]() とてしておきます。
とてしておきます。
![]() の0から10までを
の0から10までを![]() 等分して
等分して