


: 勾配を使う計算法
: 1次アルゴリズム
: 1次アルゴリズム
を例にとって説明します。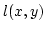 を
列ベクトルと行列
を
列ベクトルと行列
を使って表現すると
から
と書けます。
ここで,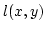 の
の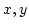 についての偏微分係数はそれぞれ,
についての偏微分係数はそれぞれ,
です。これらを要素にもつ列ベクトルは,
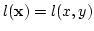 の
の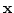 について
の微分であり,
について
の微分であり,
です。
また,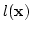 の2階微分は
の2階微分は
です。さて,
として,
結局,
となります。
無論,一般の関数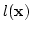 ,解析的な関数なら,
,解析的な関数なら,
となります。
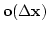 は3次以上の高位の項です。
は3次以上の高位の項です。



: 勾配を使う計算法
: 1次アルゴリズム
: 1次アルゴリズム
Yasunari SHIDAMA
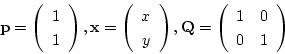
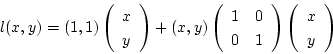
![]() の
の![]() についての偏微分係数はそれぞれ,
についての偏微分係数はそれぞれ,
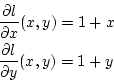
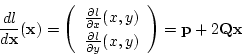
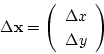
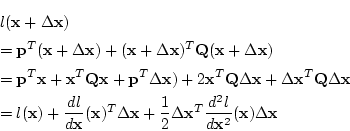
![]() ,解析的な関数なら,
,解析的な関数なら,