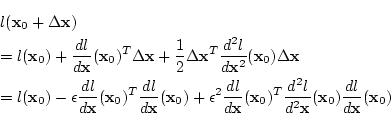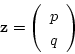: 2次アルゴリズム
: 1次アルゴリズム
: 関数の勾配
さて,
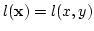 を最小化するため,先ず,
初期点
を最小化するため,先ず,
初期点
を与えて,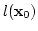 を求め,次に,
を求め,次に,
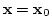 での
での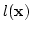 の微分,
の微分,
を求め,これと微小な正数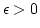 を使って,
を使って,
として,
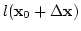 を計算すると,
を計算すると,
ここで,任意のベクトル
について
ですから,
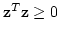 です。同様に,
です。同様に,
です。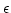 が十分小さければ,
が十分小さければ,
として,
となります。
を新たな初期点としてこれを繰り返すことができます。このような方法を勾配法といいます。特に,毎回の繰り返しで,
となるように,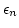 を選ぶ繰り返し計算法を最急降下法と呼びます。
を選ぶ繰り返し計算法を最急降下法と呼びます。
を繰り返しながら
を生成し,
とする計算法は,一次アルゴリズムと呼ばれています。



: 2次アルゴリズム
: 1次アルゴリズム
: 関数の勾配
Yasunari SHIDAMA
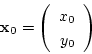
![]() での
での![]() の微分,
の微分,