


: 他段階問題
: 線形計画法
: 最大化問題
前節では線形計画法の典型的な問題を例示しました。それは制約条件
のもとで,関数
を最大化する問題でした。
条件
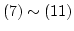 を充たす点
を充たす点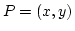 は
下のような,凸多角形の境界線も含めた内部にあります。
は
下のような,凸多角形の境界線も含めた内部にあります。

(図1.1)
この凸多角形の頂点を
とすると,
内部の点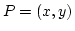 はこれらの頂点
はこれらの頂点
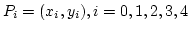 によって
によって
で表されます。これを
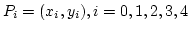 の凸結合といいます。
の凸結合といいます。
には「線形性」という性質があります。
これは
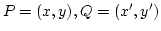
と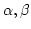 について,
について,
という性質です。この線形性を使うと,以下の議論ができます。
まず各頂点での関数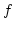
のうち最大値を
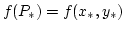 とします。すると凸多角形の内の任意の
点
とします。すると凸多角形の内の任意の
点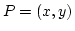 に対する
に対する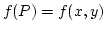 は
は
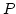 が
が
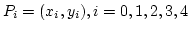 の凸結合で表されることから
の凸結合で表されることから
さらに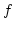 の線形性から
の線形性から
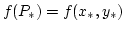 が最大で,(3)のように各
が最大で,(3)のように各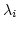 は正の数(
は正の数(
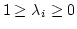 )でしたら,
)でしたら,
さらに,(2)から
で
となります。結局,関数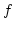 の制約条件を表す凸多角形の内部(境界を含む)の点全てを調べる必要がなく、頂点での関数
の制約条件を表す凸多角形の内部(境界を含む)の点全てを調べる必要がなく、頂点での関数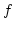 の値を調べれば良いことがが判ります。
の値を調べれば良いことがが判ります。

(図1.2)
線形化計画法の代表的な解法であるシンプレクス法はは,制約条件を表す凸多角形の頂点での関数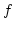 の値を効率的に調べる方法です。適当な,頂点から始め,関数
の値を効率的に調べる方法です。適当な,頂点から始め,関数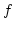 の値が増大する頂点へ次々移動して,最大解を探します。
の値が増大する頂点へ次々移動して,最大解を探します。
この他に,凸多角形の内部の点から,最大解を与える頂点を探索する内点法もあります。
これらの詳細は,後日述べます。



: 他段階問題
: 線形計画法
: 最大化問題
Yasunari SHIDAMA

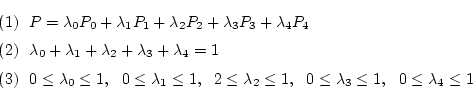
![]() について,
について,
![]()

![]() の値を効率的に調べる方法です。適当な,頂点から始め,関数
の値を効率的に調べる方法です。適当な,頂点から始め,関数![]() の値が増大する頂点へ次々移動して,最大解を探します。
の値が増大する頂点へ次々移動して,最大解を探します。