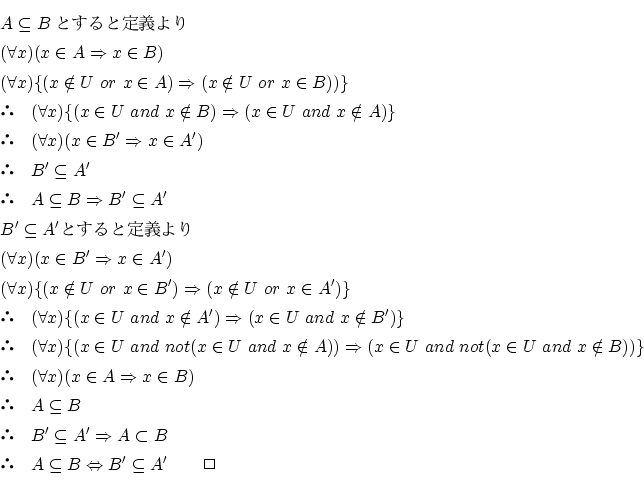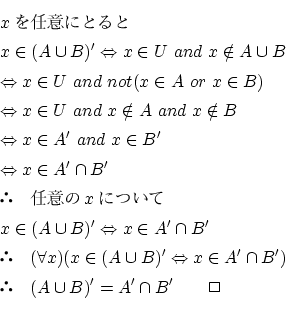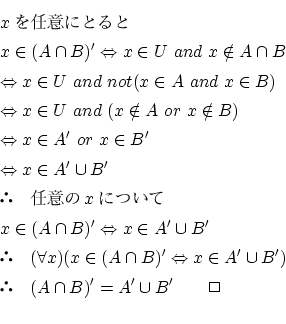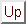


: 集合族の演算
: 合弁と共通部分
: 合弁と共通部分
目次
集合の合弁, 共通部分,補集合は以下で定義されます。
- 定義:2つの集合の和,積
-
非順序対の対公理
の公理により
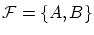 の存在が保証され,さらに合弁の公理
の存在が保証され,さらに合弁の公理
により
の存在が保証され,前節のラッセルのパラドックスを避けるための基準も充たされています。
また,前節の分出の定理
によって
関係式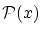 を
を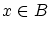 とおけば
とおけば
の存在が保証され
同様に,関係式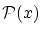 を
を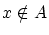 ,
, 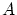 に
に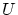 を代入すれば
を代入すれば
の存在が保証され, 何れもパラドクス回避の基準が充たされています。
これらの定義の基に以下の命題群が成り立っています。
- 命題2.2.1
-
- 証明
-
- 命題2.2.2
-
- 証明
-
- 命題2.2.3
-
- 証明
-
- 命題2.2.4
-
- 証明
-
- 命題2.2.5
-
- 証明
-
- 命題2.2.6
-
- 証明
-
- 命題2.2.7
-
- 証明
-
- 命題2.2.8
-
- 証明
-
- 命題2.2.9
-
- 証明
-
- 命題2.2.10
-
- 証明
-
- 命題2.2.11
-
- 証明
-
- 命題2.2.12
-
- 命題2.2.12の証明
-
- 命題2.2.13
-
- 証明
-
- 命題2.2.14
-
- 証明
-
- 命題2.2.15
-
- 証明
-
- 命題2.2.16
-
- 証明
-
- 命題2.2.17
-
- 証明
-
- 命題2.2.18
-
- 証明
-
- 命題2.2.19
-
- 証明
-
- 命題2.2.20
-
- 証明
-
- 命題2.2.21
-
- 証明
-



: 集合族の演算
: 合弁と共通部分
: 合弁と共通部分
目次
Yasunari SHIDAMA
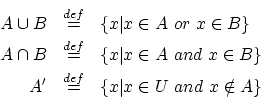
![]() を
を![]() ,
, ![]() に
に![]() を代入すれば
を代入すれば


















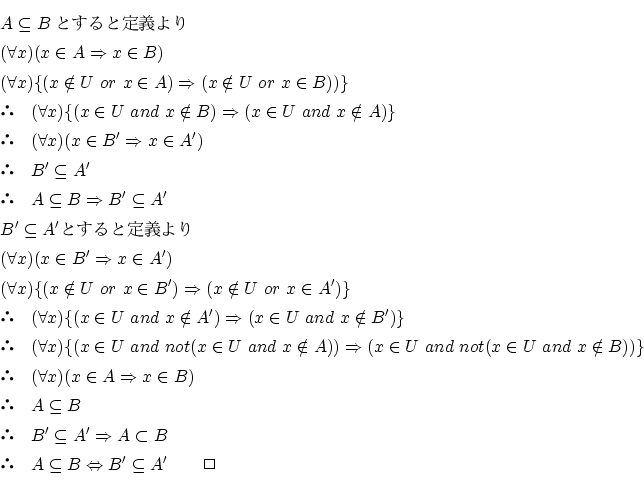
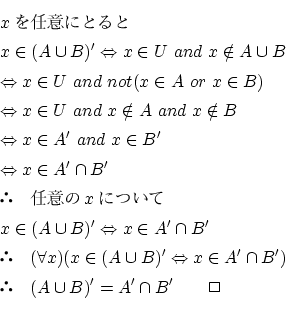
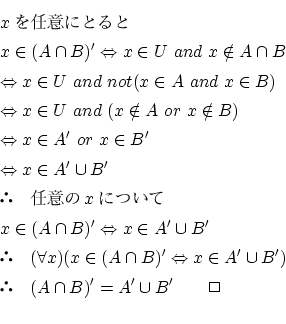
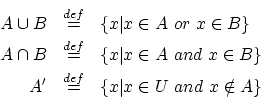
![]() を
を![]() ,
, ![]() に
に![]() を代入すれば
を代入すれば