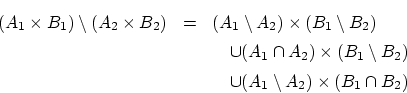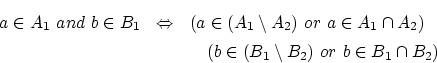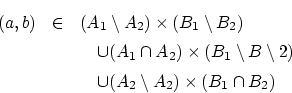


: この文書について...
: 集合の演算
: 排他和
目次
非順序対の対公理
に
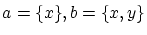 を適用して
を適用して
という集合を造れます。
この集合を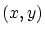 と表すことにします。
以下の性質が成立っています。
と表すことにします。
以下の性質が成立っています。
[証明]
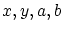 を任意にとり,
を任意にとり,
とおくと,定義から
これから
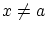 とすると
とすると
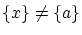 よって
よって
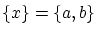
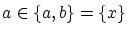 より
より 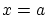 となって仮定に矛盾よって
となって仮定に矛盾よって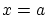
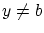 とすると
とすると
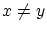 なら
なら
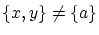 から
から
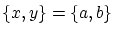
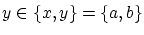 で
で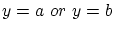
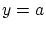 とすると
とすると 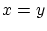 となり矛盾。しかし,
となり矛盾。しかし,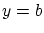 としても
としても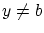 に矛盾
よって
に矛盾
よって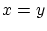
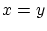 から
から
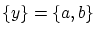 から
から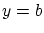 となり矛盾
となり矛盾
結局、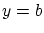
[証明終]
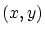 を順序対と呼びます。
を順序対と呼びます。
直積集合の定義
という集合が定義できます。これを
で表し,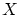 と
と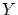 の直積と呼びます。
の直積と呼びます。
[直積集合の存在証明]
に注意すると
であり,
関係式
を
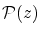 とおくと,前節の分出の定理によって
とおくと,前節の分出の定理によって
であり,さらに,
という集合が定義できます。
[証明終]
[命題2.5.1]
とすると以下が成り立つ。
-
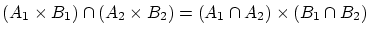
- 証明(a)
-
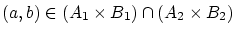 を任意に選ぶと
を任意に選ぶと
よって
同様にして
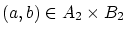 から
から
よって
よって
ゆえに任意の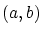 について
について
逆に
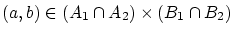 を任意に選ぶと、これから
を任意に選ぶと、これから
よって
すなわち任意の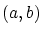 について
について
-
- 証明(b)
-
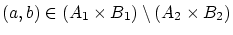 を任意に選ぶと;
を任意に選ぶと;
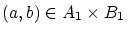 から
から
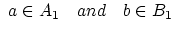
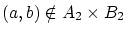 から
から
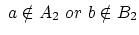
を得る。
ゆえ
となります。
逆も明か。



: この文書について...
: 集合の演算
: 排他和
目次
Yasunari SHIDAMA
![]() と表すことにします。
以下の性質が成立っています。
と表すことにします。
以下の性質が成立っています。
![]() を任意にとり,
を任意にとり,
![]() を順序対と呼びます。
を順序対と呼びます。