

: 標準形
: 記号論理
: 恒真式
中学校以来慣れ親しんでいる文字式の等式
は左辺と右辺は形の上では異なるが,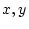 に任意の値を代入しても一致する。
この意味で
に任意の値を代入しても一致する。
この意味で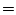 が用いられた。同様に論理式の
が用いられた。同様に論理式の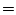 も定義できる。
も定義できる。
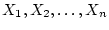 についての2つの論理式
についての2つの論理式
が与えられたとき,これらで定義される2つの真理関数
| |
|
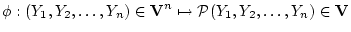 |
(1.3) |
| |
|
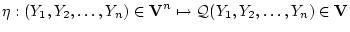 |
(1.4) |
の任意の
について(即ち
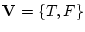 での任意の値の組み合わせについて)
常に
での任意の値の組み合わせについて)
常に
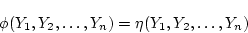 |
(1.5) |
が成り立つときに等号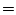 を用いて
を用いて
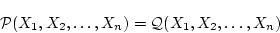 |
(1.6) |
と書くことにする。定理1.1は左辺で定義される論理式と
右辺で定義されるそれとが値が常に一致することを示し,従って今定義した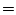 の条件をみたすことになり,以下の自明な結果が得られる。
の条件をみたすことになり,以下の自明な結果が得られる。
- 定理1.2
-
以下の論理式としての等式が成り立つ。
- (i).
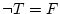 ,
, 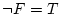
- (ii).
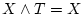 ,
, 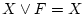
- (iii).
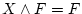 ,
, 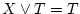
- (iv).
-
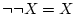 (二重否定の法則)
(二重否定の法則)
- (v).
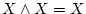 ,
, 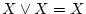 (巾等律)
(巾等律)
- (vi).
-
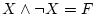 (矛盾律),
(矛盾律),
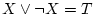 (排中律)
(排中律)
- (vii).
-
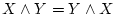 ,
,
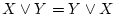 (交換法則)
(交換法則)
- (viii).
-
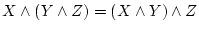 (結合法則)
(結合法則)
- (ix).
-
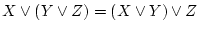 (結合法則)
(結合法則)
- (x).
-
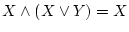 (吸収法則)
(吸収法則)
- (xi).
-
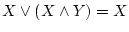 (吸収法則)
(吸収法則)
- (xii).
-
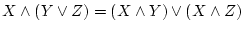 (分配法則)
(分配法則)
- (xiii).
-
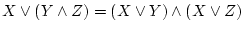 (分配法則)
(分配法則)
- (xiv).
-
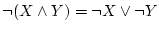 (ド・モルガンの法則)
(ド・モルガンの法則)
- (xv).
-
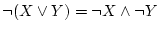 (ド・モルガンの法則)
(ド・モルガンの法則)
- (xvi).
-
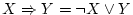


: 標準形
: 記号論理
: 恒真式
Yasunari SHIDAMA
![]() についての2つの論理式
についての2つの論理式
![]() を用いて
を用いて