|
|
|
||||
で
![]() が
が![]() とも同じ値のときのみ
とも同じ値のときのみ![]() になることに
注目すれば右辺と左辺の真理表を作ってそれが一致することを確かめればよい。
ここでは、(xii) と (xv) と (xvi) についてのみ示し、他は課題とする。
になることに
注目すれば右辺と左辺の真理表を作ってそれが一致することを確かめればよい。
ここでは、(xii) と (xv) と (xvi) についてのみ示し、他は課題とする。
目的の式の右辺と左辺の真理表とともに補助的に、![]() ,
,
![]() ,
, ![]() ,
, ![]() の真理表も作れば次のようにな
る。
の真理表も作れば次のようにな
る。
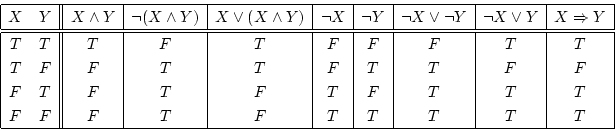
上の表から、(10) の左辺
![]() と右辺
と右辺 ![]() の真理表、
(14) の左辺
の真理表、
(14) の左辺
![]() と右辺
と右辺
![]() の真理表、
および、(16) の左辺
の真理表、
および、(16) の左辺
![]() と右辺
と右辺 ![]() の真
理表は、確かにそれぞれ一致している。
の真
理表は、確かにそれぞれ一致している。
![]()