


: 変数式の標準形
: 標準形
: 基本式
さて,上の
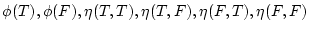 は何れも
は何れも
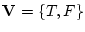 の元でありそれぞれの値によって,
式がさらに短くなる。
の元でありそれぞれの値によって,
式がさらに短くなる。
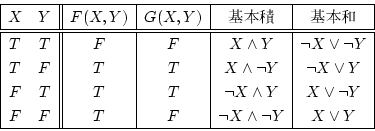
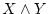 などを基本積と呼ぶことにすると、
以下のように
などを基本積と呼ぶことにすると、
以下のように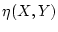 の真理値とそれに付随する基本積の表
の真理値とそれに付随する基本積の表
を作成し,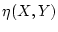 の真理値
の真理値
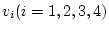 が
が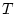 となる基本積
のみの論理和
となる基本積
のみの論理和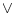 で結合した論理式に等しいことがわかる。
これを
主
で結合した論理式に等しいことがわかる。
これを
主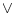 標準形という。
標準形という。
また,同様に
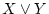 などを基本和と呼ぶことにすると。
以下のように
などを基本和と呼ぶことにすると。
以下のように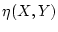 の真理値とそれに付随する基本和の表
の真理値とそれに付随する基本和の表
を作成し,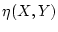 の真理値
の真理値
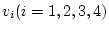 が
が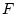 となる基本和
のみの論理積
となる基本和
のみの論理積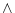 で結合した論理式に等しいことがわかる。これを
主
で結合した論理式に等しいことがわかる。これを
主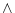 標準形という。
標準形という。
例をみよう。
なる2変数真理関数 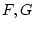 を主
を主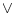 -標準形で表わせば、次のようになる:
-標準形で表わせば、次のようになる:
- [
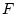 の主
の主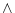 -標準形]
-標準形]
第1行だけに着目する。
第1行に対して
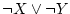
1項しかないので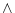 で結合するまでもなく。
で結合するまでもなく。
が得られる。
- [
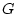 の主
の主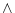 -標準形]
-標準形]
第1,4行に着目する。
第1行に対して
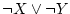 をつくる。
第4行に対して
をつくる。
第4行に対して 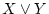
これらを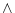 で結合すれば
で結合すれば
が得られる。

- [
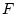 の主
の主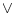 -標準形]
-標準形]
第2,3,4行に着目する。
第2行に対して
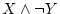 をつくる。
第3行に対して
をつくる。
第3行に対して
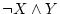
第4行に対して
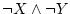
これらを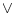 で結合すれば
で結合すれば
が得られる。
- [
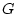 の主
の主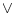 -標準形]
-標準形]
第2,3行に着目する。
第2行に対して
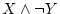 をつくる。
第3行に対して
をつくる。
第3行に対して
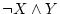
これらを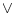 で結合すれば
で結合すれば
が得られる。




: 変数式の標準形
: 標準形
: 基本式
Yasunari SHIDAMA
![]() などを基本積と呼ぶことにすると、
以下のように
などを基本積と呼ぶことにすると、
以下のように![]() の真理値とそれに付随する基本積の表
の真理値とそれに付随する基本積の表
![]() などを基本和と呼ぶことにすると。
以下のように
などを基本和と呼ぶことにすると。
以下のように![]() の真理値とそれに付随する基本和の表
の真理値とそれに付随する基本和の表
![]()
![]() で結合するまでもなく。
で結合するまでもなく。
![]() で結合すれば
で結合すれば
![]() で結合すれば
で結合すれば