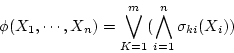: よく用いられる真理関数
: 標準形
: 変数式の標準形
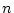 変数真理関数を表わす論理式についても,前節の
変数真理関数を表わす論理式についても,前節の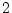 変数の方法を拡張して
次の定理のように標準形を作ることができる。
以下では,表現を簡単にするため
変数の方法を拡張して
次の定理のように標準形を作ることができる。
以下では,表現を簡単にするため
| |
|
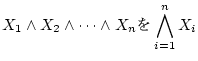 |
(1.14) |
| |
|
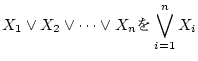 |
(1.15) |
と書く。
- 定理2.2
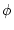 を
を 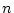 変数真理関数とする。
変数真理関数とする。
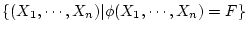 を
を
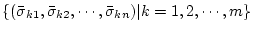 とし、
とし、
とおけば、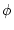 の主
の主 標準形(principal disjunctivenormal form)
による表現が与えられる。
標準形(principal disjunctivenormal form)
による表現が与えられる。
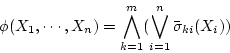 |
(1.16) |
- 課題
-
主 標準形が
標準形が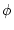 を表現する論理式であること、すなわち、
を表現する論理式であること、すなわち、
が成立することを示せ。
定理2.2と相対な次の定理も得られる:
- 定理2.3
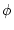 を
を 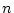 変数真理関数とする。
変数真理関数とする。
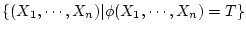 を
を
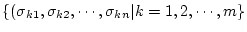 とし、
とし、
とおけば、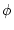 の主
の主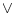 -標準形(principal conjunctive
normal form)
-標準形(principal conjunctive
normal form)
が得られる。
- 主
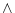 -標準形 を導くアルゴリズム
-標準形 を導くアルゴリズム
-
与えられた 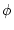 の真理表から、主
の真理表から、主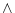 -標準形 を導くアルゴ
リズムを述べる。
-標準形 を導くアルゴ
リズムを述べる。
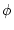 の真理表
の真理表
に対し、
- (1).
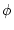 の関数値
の関数値 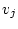 が
が 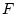 である行に着目する。(定理の前提
から
である行に着目する。(定理の前提
から 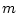 行ある。)
行ある。)
- (2).
- (1) で着目した各行について、
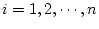 に対し、
に対し、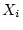 の値が
の値が 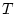 ならば
ならば 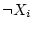 を、
を、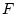 ならば
ならば 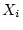 をつくってこれらを
をつくってこれらを 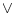 で結ぶ。(これにより、
で結ぶ。(これにより、
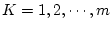 につい
て、
につい
て、
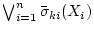 ができる。)
ができる。)
- (3).
- (2) でつくられた
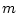 個の各式を
個の各式を 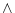 で結ぶ。(これによって、
で結ぶ。(これによって、
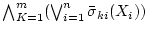 が得られる。)
が得られる。)
- 課題
-
が成立することを示せ。
- 定理3
-
全ての真理関数は
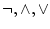 の3種類の論理記号のみを用いた
論理式で表現できる。
の3種類の論理記号のみを用いた
論理式で表現できる。
- 証明
-
標準形の定理2.2,定理2.3から明らかである。
さらに以下の定理が成立つ。
- 定理4
-
- (1)
- 全ての論理式(真理関数)は論理記号
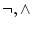 のみを用いた論理式で表現できる。
のみを用いた論理式で表現できる。
- (2)
- 全ての論理式(真理関数)は論理記号
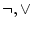 のみを用いた論理式で表現できる。
のみを用いた論理式で表現できる。
- 証明
-
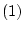 の証明:定理1.2の2重否定の法則
とドモルガンの法則を用いれば
の証明:定理1.2の2重否定の法則
とドモルガンの法則を用いれば
であるから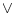 は
は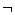 と
と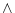 によって表現できる。
このことと定理4から
によって表現できる。
このことと定理4から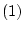 が得られる。
が得られる。
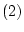 の証明:定理2.2のの2重否定の法則
とドモルガンの法則を用いれば
の証明:定理2.2のの2重否定の法則
とドモルガンの法則を用いれば
このことと定理4から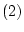 が得られる。
が得られる。




: よく用いられる真理関数
: 標準形
: 変数式の標準形
Yasunari SHIDAMA
![]() 変数真理関数を表わす論理式についても,前節の
変数真理関数を表わす論理式についても,前節の![]() 変数の方法を拡張して
次の定理のように標準形を作ることができる。
以下では,表現を簡単にするため
変数の方法を拡張して
次の定理のように標準形を作ることができる。
以下では,表現を簡単にするため
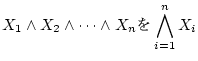
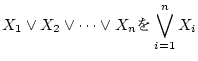
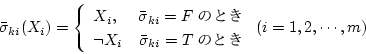
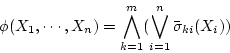
![]() 標準形が
標準形が![]() を表現する論理式であること、すなわち、
を表現する論理式であること、すなわち、
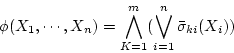
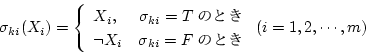
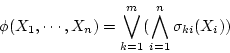
![]() の真理表
の真理表