ここで,
集合![]() やそれから作られる
やそれから作られる![]() 次元数ベクトル空間
次元数ベクトル空間![]() について復習してみます。
について復習してみます。
![]() についてはそれらの要素の間に加算と乗法が定義され以下が成り立っていました。
についてはそれらの要素の間に加算と乗法が定義され以下が成り立っていました。

![]() についても
についても![]() のように要素間に加法が定義されていました。
のように要素間に加法が定義されていました。
![]() のように要素の間の
乗法は定義されませんが,
のように要素の間の
乗法は定義されませんが,![]() との
との![]() の乗法が定義され,以下が成り立っていました。
の乗法が定義され,以下が成り立っていました。
![]() の要素
の要素
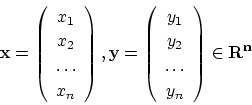
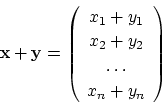
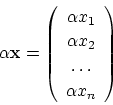
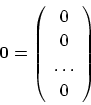
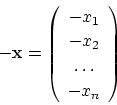
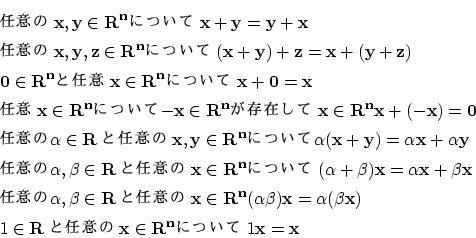
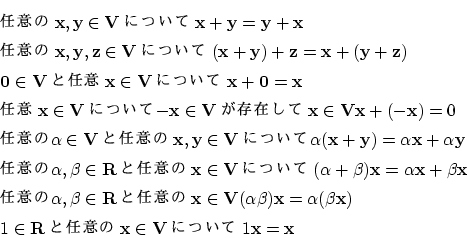
さて,線形空間は数ベクトル空間に限りません。関数の集合もベクトル空間になります。
ここで調べようとしている関数の集合![]() も同様な数学的な構造をもっています。
まず,
も同様な数学的な構造をもっています。
まず,
上の式の意味は![]() の任意の元
の任意の元![]() に対して
に対して![]() を対応させる関数で関数
を対応させる関数で関数![]() を定義するという意味です。
を定義するという意味です。
同様に,
![]() と
と
![]() の乗法
の乗法![]() は
は
全く同様に
![]() ,
,
![]() もそれぞれ
もそれぞれ
[問題3.1]
![]() として,線形空間の条件を充たしていることを確認してください。
として,線形空間の条件を充たしていることを確認してください。