![]() が
が![]() 上の線形空間であるとします。すなわち,
上の線形空間であるとします。すなわち,
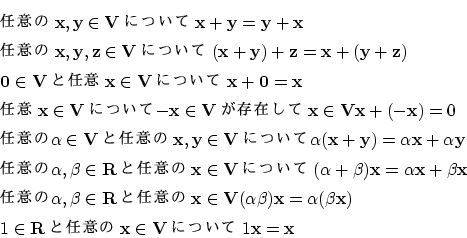
が成り立っているものとします。
ここで,![]() の部分集合
の部分集合
![]() について
について

が成り立っているとき
![]() も
も![]() 上の線形空間になっています。
上の線形空間になっています。![]() を
を![]() の部分線形空間といいます。
の部分線形空間といいます。
[問題3.2] ![]() が上の条件を充たすとき線形空間になっていることを確かめてください。
が上の条件を充たすとき線形空間になっていることを確かめてください。
[例1]
![]() でからへの連続な関数の集合を表すとき,すなわち,
でからへの連続な関数の集合を表すとき,すなわち,
のとき,![]() は
は
![]() の部分線形空間です。
の部分線形空間です。
[証明]
復習すが,関数
![]() が
が![]() 上で連続というのは
上で連続というのは
「任意の![]() について,任意の正数
について,任意の正数![]() に対して,これらに依存したある正数
に対して,これらに依存したある正数
![]() が存在して
が存在して
が成り立つ」ということでした。
![]() は
は![]() 上で連続でしたので,
任意の
上で連続でしたので,
任意の![]() について,任意の正数
について,任意の正数
![]() に対して
に対して
それぞれ,
が成り立っています。
すると,
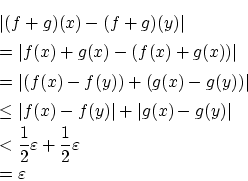
![]() なら
なら![]() です。
です。
![]() は
は![]() 上で連続でしたので,
任意の
上で連続でしたので,
任意の![]() について,任意の正数
について,任意の正数![]() に対して
に対して
が成り立っています。
すると,
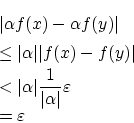
[例2]前章にもでてきた,![]()
![\begin{eqnarray*}
&&C^1[0,1]=\{f\vert f:[0,1]から{\bf R}への関数,[0,1]で微分可能,\\
&&その導関数x\in [0,1] \mapsto f'(x)がxについて連続。\}
\end{eqnarray*}](img96.gif)
[証明]
まず微積分の復習から。
関数
![]() が
が ![]() で微分可能であるとは次の極限値
で微分可能であるとは次の極限値
で表しました。
さらに,任意の![]() で微分可能であるとき
関数
で微分可能であるとき
関数![]() は
は ![]() 上で微分可能であるといいました。
上で微分可能であるといいました。
を導関数と呼びました。さらに,この導関数が![]() 上連続のとき,すなわち
上連続のとき,すなわち
結局,以上の定義を使って書き直せば,
さらに定義から,![]() は
は![]() 上微分可能かつ
上微分可能かつ
また,任意の![]() にいて,
にいて,

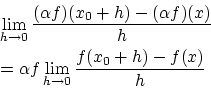
となることから,
![]() は
は![]() 上微分可能で,
上微分可能で,