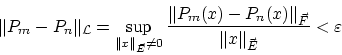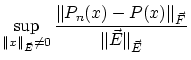


: この文書について...
: 最適化理論-変分法と微分その4-
: 目次
目次
前章で
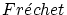 微分
微分
を定義しましたがたが,これは
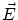 から
から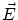 への連続線形写像でした。
への連続線形写像でした。
最後にこの章で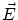 から
から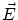 への連続線形写像全体の
空間の構造について調べておきましょう。
への連続線形写像全体の
空間の構造について調べておきましょう。
とし,
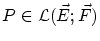 のノルムを
のノルムを
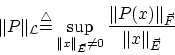 |
(0.1) |
と定義します。
[定理]
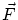 がBanach空間ならば
がBanach空間ならば
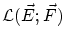 は
Banach空間になる。
は
Banach空間になる。
証明
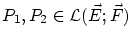 とすれば,
任意の
とすれば,
任意の
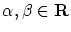 について,
について,
です。従って,
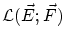 は線形空間です。
は線形空間です。
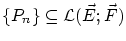 が
が
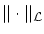 ノルムの意味でCaushy列と仮定すると
ノルムの意味でCaushy列と仮定すると
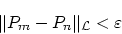 |
(0.2) |
(1)より
これより
したがって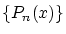 は
は
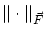 ノルムの意味で
Caushy列となります。
ノルムの意味で
Caushy列となります。
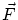 はBanach空間ですから、完備なので
はBanach空間ですから、完備なので
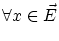 に対して
に対して
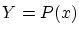 とおくと
とおくと
ゆえに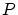 の線形性が示されました。
の線形性が示されました。
次に連続であることを示します。(2)より
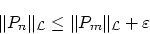 |
(0.3) |
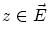 に対して
に対して
とすると
よって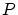 は連続となります。結局
は連続となります。結局
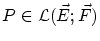 です。
です。
したがって
ゆえに(1),(4)より
以上より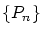 は収束するので完備性が示されました。
は収束するので完備性が示されました。
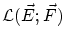 はノルム空間ですからBanach空間になっています。
はノルム空間ですからBanach空間になっています。

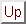


: この文書について...
: 最適化理論-変分法と微分その4-
: 目次
目次
Yasunari SHIDAMA
![]() がBanach空間ならば
がBanach空間ならば
![]() は
Banach空間になる。
は
Banach空間になる。
![]() とすれば,
任意の
とすれば,
任意の
![]() について,
について,
![]() が
が
![]() ノルムの意味でCaushy列と仮定すると
ノルムの意味でCaushy列と仮定すると