![]() を体とし,
を体とし, ![]() を
を ![]() 上の線形空間とする.
上の線形空間とする. ![]() を
を ![]() の部分空間全体の
集合とする.(線形空間,線形空間の部分空間の説明は省略します.)このとき,
の部分空間全体の
集合とする.(線形空間,線形空間の部分空間の説明は省略します.)このとき,
![]() を任意にとると,
を任意にとると, ![]() は
は ![]() の部分線形空間で
の部分線形空間で
![]() も部分線形空間.
も部分線形空間.
(実際,
![]() を任意にとると,
を任意にとると,
![]() ゆえ
ゆえ
![]() が
が ![]() の下界とすると;
の下界とすると;
![]() を任意にとると,
を任意にとると,
![]() から
から
![]() で
で
![]()
よって,
![]()
![]() は有限個の
は有限個の
![]() の元,
の元,
![]() は有限個の
は有限個の ![]() の元
の元 ![]()
とおくと, ![]() は
は ![]() の部分線形空間,
の部分線形空間,
(実際
![]() を任意にとると,
を任意にとると,
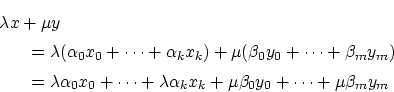
よって
ゆえに,
![]() を
を ![]() の部分線形空間として,
の部分線形空間として, ![]() の上界,
すなわち
の上界,
すなわち
![]() とすると,
とすると,
![]() を任意にとると,
有限個の
を任意にとると,
有限個の
![]() が存在して
が存在して
結局,
[(1)の証明終]
![]() を任意にとると,
を任意にとると, ![]() の定義から
の定義から
![]() を任意にとると
を任意にとると ![]() よって
よって
任意の ![]() について
について
![]() で,
で, ![]() は
は ![]() の下界.
の下界.
![]() が
が ![]() の下界とすると;
の下界とすると;
![]() を任意にとると,
を任意にとると,
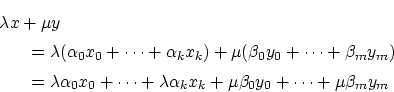
作り方から
![]() で
で ![]() は
は
![]() の上界.
の上界.
![]() を
を ![]() の部分線形空間として,
の部分線形空間として, ![]() の上界,すなわち,
の上界,すなわち,
![]() とすると
とすると
![]() を任意にとると,
有限個の
を任意にとると,
有限個の
![]() が存在して
が存在して