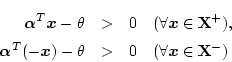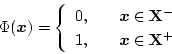
なるパーセプトロン
が存在するための必要十分条件は
その平面
で定義される。
解の構成法については次の 「学習アルゴリズム」 が知られています。
- START
-
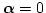 とおく。
とおく。 - TEST
-
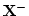 または
または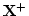 に属する
に属する
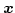 を一つとる。
を一つとる。
-
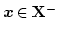 ならば
ならば
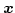 に
に
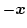 を代入する。
を代入する。 -
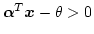 ならば TESTへ,そうでなければ ADDへ
ならば TESTへ,そうでなければ ADDへ
- ADD
-
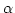 に
に
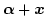 を代入し, TESTへ
を代入し, TESTへ
以上によって,構成したい論理関数が線形分離可能ならば,それを実現するパーセプトロンは,有限回の学習によって構築できます。 以下,この定理の証明を書きます。
とおきます。 ここで,任意の
ですから
は常に成り立っています。
ここで
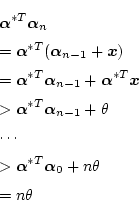
tonarimasu となります。 次に分母を調べと
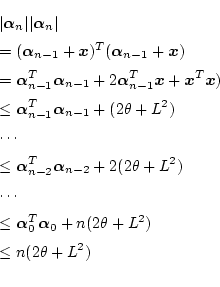
です。 これから
となります。これら分母,分子の評価式から
を得て,