


: 集合論での定理の証明
: 記号論理
: 演繹定理,全称化,特称化
目次
集合論では今まで述べた「述語論理の公理」に集合論の固有の公理が加わります。
これらは,述語論理の恒真式の集まりである公理と異なり,真であると仮定する関係式です。
以下にそれを述べておきましょう。これは公理系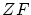 (Zermero, Fraenkelの公理系)
と呼ばれるものです。
(Zermero, Fraenkelの公理系)
と呼ばれるものです。
- 外延性の公理
これは,二つの集合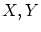 が「等しい」ことの定義を与えます。
が「等しい」ことの定義を与えます。
- 非順序対の対公理
これは,二つの対象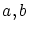 が与えらときに,これら要素からなる集合
が与えらときに,これら要素からなる集合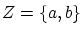 の存在することを示します。
の存在することを示します。
- 合弁の公理
これは例えば,複数の集合の集合
が与えられたときに,これらの全ての合弁
が存在することを示します。
- 空集合の存在公理
要素を一つも持たない集合の「存在」を意味します。そのような集合は,後で説明しますが,唯一ですので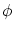 で表すことにします。
で表すことにします。
- べき集合の公理
これは集合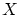 が与えられたときにその
が与えられたときにその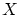 の部分集合全体からなる集合の存在を
示しています。そのような集合を
の部分集合全体からなる集合の存在を
示しています。そのような集合を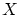 のべき集合と呼びます。
例えば
のべき集合と呼びます。
例えば
のとき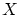 のべき集合は
のべき集合は
です。
- 無限集合の存在公理
- 正則性の公理
これは,空でない集合で,それ自身の要素との共通部分が空でないというような
「病的な集合」は存在しないということを意味します。
選択公理
集合族
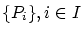 について,
について,
について:
のとき,
集合論では以下の推論規則が追加されます。
- 置換の推論規則
ただし関係式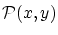 には
には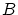 は現れないものとします。
これは関係式
は現れないものとします。
これは関係式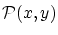 を用いて関数を定義するときなどに用います。
を用いて関数を定義するときなどに用います。
ただし関係式
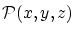 には
には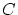 は現れないものとします。
は現れないものとします。



: 集合論での定理の証明
: 記号論理
: 演繹定理,全称化,特称化
目次
Yasunari SHIDAMA
![]() (Zermero, Fraenkelの公理系)
と呼ばれるものです。
(Zermero, Fraenkelの公理系)
と呼ばれるものです。
![]() が「等しい」ことの定義を与えます。
が「等しい」ことの定義を与えます。
![]() が与えらときに,これら要素からなる集合
が与えらときに,これら要素からなる集合![]() の存在することを示します。
の存在することを示します。
![]() について,
について,
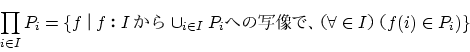
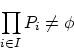
![]() には
には![]() は現れないものとします。
は現れないものとします。