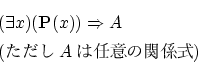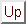


: 集合論の公理系
: 記号論理
: 推論規則
目次
前節のような公理と推論規則の対は公理系と呼ばれます。
前節の系を で表すことにします。
で表すことにします。
関係式 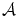 が証明可能であるとは,
が証明可能であるとは,
 において,公理系
において,公理系 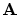 から
から 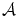 が推論規
則によって導けることですから,これを
が推論規
則によって導けることですから,これを
と書きます。推論規則
はこの表記法を用いると,
と書くべきです。しかし,煩雑さを避けるため,どの系で証明可能なのか明らかな場合は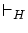 は省略することにします。
は省略することにします。
- 演繹定理は「推論規則」同様,有用な道具を提供します。
演繹定理
公理系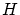 の公理に関係式
の公理に関係式
を追加してできる新たな系で
関係式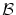 が証明可能であるとき,このことを
が証明可能であるとき,このことを
で表します。このとき:
が成り立ちます。
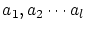 は
は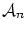 に現われる総ての自由変数記号
とします。
に現われる総ての自由変数記号
とします。
特に,関係式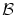 の中で,
の中で,
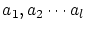 が
が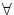 で束縛されていない
自由変数[
で束縛されていない
自由変数[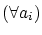 のような記号がないという意味です。]
ならば
のような記号がないという意味です。]
ならば

これから,背理法として知らる有用な道具が得られます。
背理法
ある関係式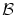 が存在して,
が存在して,
ならば

特に限定記号のある関係式については
ならば
ならば
また以下の推論規則も有用です。
- 全称化
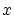 が
が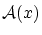 の自由変数であれば,
の自由変数であれば,
- 特称化
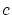 が特定の対象を表す対象定数記号とするとき,
が特定の対象を表す対象定数記号とするとき,
定理
以上の,公理,推論法則を使えば次の諸定理を得ます。「定理」とは証明可能な
関係式のことです。
- ((a))
- 関係式
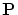 について
について
- 任意の対象
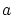 に対し
に対し
は定理です。
- 任意の自由変数
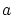 に対し
に対し
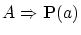 が定理ならば
が定理ならば
も定理です。
- 任意の対象
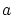 に対し
に対し
は定理です。
- ある対象
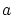 に対し
に対し
が定理ならば
も定理です。
- ((b))
- 関係式
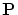 と
と 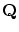 について
について
-
は定理です。
-
は定理です。
- ((c))
-
- 束縛変数を含む関係式
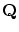 において,その束縛変数記号を
において,その束縛変数記号を 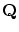 に含
まれない他の束縛変数記号でおきかえて得られます関係式を
に含
まれない他の束縛変数記号でおきかえて得られます関係式を 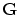 とすれば,
とすれば,
は定理です。 たとえば,
は定理です。
- 関係式
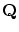 において,ひき続いて現れる同種の限定記号の順序を変
更して得らる関係式を
において,ひき続いて現れる同種の限定記号の順序を変
更して得らる関係式を 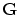 とすれば,
とすれば,
は定理です。
たとえば,
は定理です。
-
は定理です。
-
は定理です。
- ((d))
- 関係式
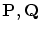 について,以下は
定理です。
について,以下は
定理です。



: 集合論の公理系
: 記号論理
: 推論規則
目次
Yasunari SHIDAMA
![]() で表すことにします。
で表すことにします。
![]() が証明可能であるとは,
が証明可能であるとは,
![]() において,公理系
において,公理系 ![]() から
から ![]() が推論規
則によって導けることですから,これを
が推論規
則によって導けることですから,これを
![]() の公理に関係式
の公理に関係式