集合論での定理の証明

集合論などの数学的理論では1.2節の公理まで遡って,定理の証明を記述することはあまりません。その記述では暗黙のうちに1.2,1.3節で述べた推論法則や,演繹定理を使い,その推論がどの推論法則を使っているかでさえ,明示しません。 ここで,いくつか典型的な類例を挙げておきます。

1. 例えば,
   
   $$(\forall x)(x \in A \Rightarrow x \in B)$$
   
   
   を証明するには以下のようになります。
   1. 先ず,任意の対象（変数）記号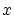$x$を選ぶ。
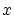      実際には,「$x$を任意にとる。」などと記述されます。

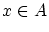   2. $x \in A$を仮定する。
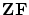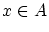      これは今扱っている集合論の公理系（これを${\bf ZF}$としておきます。） に関係式$x \in A$を追加し,
      以後この新しい公理系（これを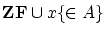 ${\bf ZF} \cup x \{\in A \}$としておきます。）で議論を意味します。
      

      実際には,「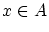$x \in A$を仮定すると」などと書きます。

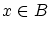   3. $x \in B$を示す。 これは,
      
      $${\bf ZF} , \{x \in A \} \vdash_H x \in B$$
      
      
      意味します。
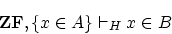
   4. (c)から演繹定理により,
      
      $${\bf ZF} \vdash_H (x \in A) \Rightarrow (x \in B)$$
      
      
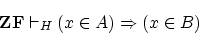
      が示されます。
      

      実際には,
      「仮定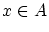$x \in A$により
      

      $$(x \in A) \Rightarrow (x \in B)$$
      
      
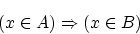
      」 などと記述されます。

   5. (d)の結果について,(a)で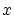$x$は任意に選択されているので自由変数であり,推論規則「全称化」を適用します。

      実際には,
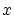      「$x$は任意であったから
      

      $$(\forall x)(x \in A) \Rightarrow (x \in B)$$
      
      
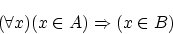
      」 などと記述されます。

2. 
   
   $$(\exists x)(x \in A) \Rightarrow {\bf P}$$
   
   
   を証明するには以下のようになります。${\bf P}$は何らかの関係式です。
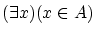   1. 先ず, $(\exists x)(x \in A)$を仮定する。
      実際には「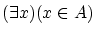 $(\exists x)(x \in A)$を仮定する。」などと記述されます。
      これは今扱っている集合論の公理系に関係式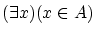 $(\exists x)(x \in A)$を 追加し,以後この新しい公理系での議論を意味します。 ぶ。
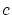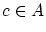   2. $c$を$c \in A$ を充たす定数（対象定数記号）とする。
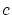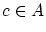      「$c$を$c \in A$を充たす対象とする」などと書かれます。
      

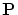   3. ${\bf P}$を示す。

      
      

      $${\bf ZF} , (\exists x)(x \in A)　\vdash_H {\bf P}$$
      
      
      意味します。
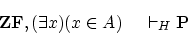
   4. (c)から演繹定理により,
      
      $${\bf ZF} \vdash_H (\exists x)(x \in A) \Rightarrow {\bf P}$$
      
      
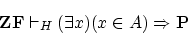
      が示されます。
      

      実際には,
      「仮定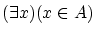 $(\exists x)(x \in A)$により
      

      $$(\exists x)(x \in A) \Rightarrow {\bf P}$$
      
      
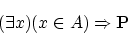
      」 などと記述されます。