


: 公理系と推論規則
: 記号表現
: 恒真式
目次
前項では真偽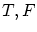 を決める代数的方法を見ましたが,これには「限界」がありました。
を決める代数的方法を見ましたが,これには「限界」がありました。
ここで,中学校時代に習ったと思いますが,三角形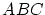 の内角の和が180°であることを示す平面幾何の証明を思い出しましょう。これを示すには例えば,
の内角の和が180°であることを示す平面幾何の証明を思い出しましょう。これを示すには例えば,
- 問題の三角形底辺の底辺を
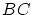 として,それを右端点
として,それを右端点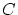 から適当な長さだけ右へ
延長し端点を
から適当な長さだけ右へ
延長し端点を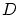 としておく。
としておく。
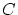 を通り,斜辺
を通り,斜辺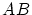 に平行な補助線を引く。これを
に平行な補助線を引く。これを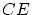 とする。
とする。
- 平行線と交差する直線と交わる角度についての性質から
によって内角の和が180°であることを「証明」しました。
この証明を記号で表現すれば,
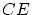 は
は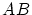 に平行。(公理)
に平行。(公理)
- 2本の平行線と交わる直線がつくる2つの同位角は等しい。(公理)
- 従って,
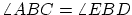
- 2本の平行線と交わる直線がつくる2つの叉角は等しい。(公理)
- 従って,
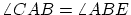
- 直線は180°である。(公理)
- 等しい角度どうしを足し合わせても結果は等しい(公理)
- 結論
という表現でしょう。これをさらにメタ記号を使って
表して,詳しく記述すれば,
となるでしょう。
1番目から3番目までの式を見ると
という3段論法がでてきます。同様に4番目の式も
という3段論法によっていることが判ります。
6番目の式
は例えば,
という関係式が既に正しいものとして認められていれば,
という2回の3段論法の適用によって与えられることが判ります。
5番目以降の式も同様です。
は
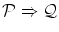 と記号
と記号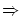 の前にある
の前にある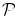 から記号
から記号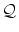 を取り出す記号操作です。
を取り出す記号操作です。
と
が前項で述べた恒真式なら
も恒真式になります。3段論法などの操作の規則を推論規則と呼びますが,この推論規則を用いれば既に判っている真な関係式から新たに真な関係式を作り出すことができます。
その推論規則を適用して,関係式が導かれる過程を書いたものが「証明」です。
前節に挙げた,少数の恒真式(命題論理の公理)からも推論規則によって無数の恒真式を作り出すことができます。
この方法なら,関係式が
や
のようなものを含んでいても真偽を示すことができます。
関係式
が正しいもと判っていれば,これの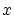 に特定の対象,例えば
に特定の対象,例えば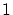 などを代入して
などを代入して
が正しいことが判り,
逆に,
が正しいことが判っていれば,
が正しいことが判りますので,
や
などの関係式についての操作の規則を定めておけば,これらの関係式を
含んだものについても,真であることを示すことができます。このような規則としては他に,例えば,以下のものもあります。
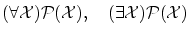 は前節の式の定義を観ればわかるように何れの場合も,
は前節の式の定義を観ればわかるように何れの場合も,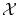 は見かけ上の変数にすぎません。
は見かけ上の変数にすぎません。
そこで「関係式
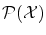 の中に
の中に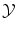 という変数が使われていなければ.
という変数が使われていなければ.
という書き換えができる」という規則を定めることができます。
結局,少数の自明とされる関係式あるは,真と仮定するので証明不要とする関係式の集まり(これを公理と呼びます)と,それらを使って,新たな「正しい」関係式を導き出す規則を定めておけば良いということが判ります。
以上のように記号論理学では,対象にしている関係式(論理式とも言います)が正しい主張の内容を表しているかどうかを決定する方法や,正しい論理式から別の正しい論理式を導く法則を研究します。
次にこの資料で用いるその公理について述べていきましょう。



: 公理系と推論規則
: 記号表現
: 恒真式
目次
Yasunari SHIDAMA
![]() を決める代数的方法を見ましたが,これには「限界」がありました。
を決める代数的方法を見ましたが,これには「限界」がありました。
![]() の内角の和が180°であることを示す平面幾何の証明を思い出しましょう。これを示すには例えば,
の内角の和が180°であることを示す平面幾何の証明を思い出しましょう。これを示すには例えば,
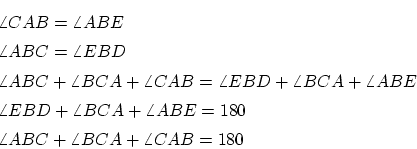
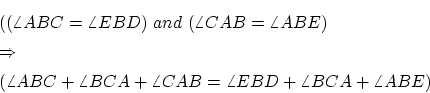
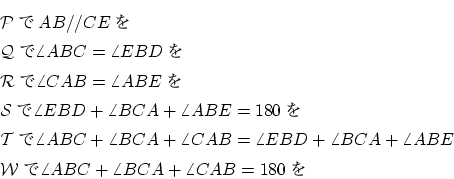
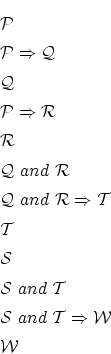
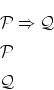
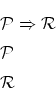
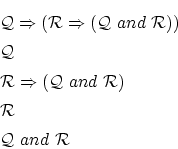
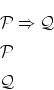
![]() は前節の式の定義を観ればわかるように何れの場合も,
は前節の式の定義を観ればわかるように何れの場合も,![]() は見かけ上の変数にすぎません。
は見かけ上の変数にすぎません。
![]() の中に
の中に![]() という変数が使われていなければ.
という変数が使われていなければ.