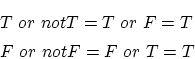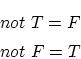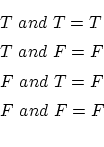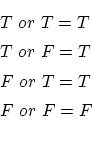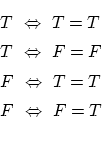


: 推論
: 記号表現
: 真理値
目次
関係式
について考えてみます。
これは 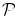 が
が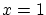 を表しているものとすれば
を表しているものとすれば
という関係式を表しています。前項の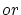 と
と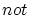 の真理値の計算結果を用いると
の真理値の計算結果を用いると
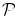 が
が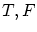 どちらの値をとっても
どちらの値をとっても
で恒に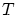 となります。
関係式
となります。
関係式
は、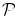 が
が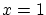 などどのような関係式を表していようと,また,真偽
などどのような関係式を表していようと,また,真偽
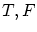 どちらであろうと,恒に真
どちらであろうと,恒に真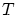 となります。このように関係式には,恒に真
となります。このように関係式には,恒に真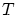 となるものがあり,これは恒真式と呼ばれます。恒真式は他にもあり例えば以下のものが知られています。
となるものがあり,これは恒真式と呼ばれます。恒真式は他にもあり例えば以下のものが知られています。
-
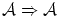
-
![$\cal (A \Rightarrow B)
\Rightarrow [(B \Rightarrow C) \Rightarrow (A \Rightarrow C)]$](img85.png)
-
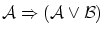
-
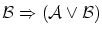
-
![$\cal (A \Rightarrow C)
\Rightarrow \{ (B \Rightarrow C)
\Rightarrow [(A \lor B) \Rightarrow C]\}$](img88.png)
-
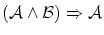
-
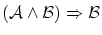
-
![$\cal (C \Rightarrow A)
\Rightarrow \{ (C \Rightarrow B)
\Rightarrow [C \Rightarrow (A \land B)]\}$](img91.png)
-
![$\cal [A \land (A \Rightarrow B)] \Rightarrow B$](img92.png)
-
![$\cal [(A \land C) \Rightarrow B]
\Rightarrow [C \Rightarrow (A \Rightarrow B)]$](img93.png)
-
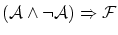
-
![$\cal [(A \land B) \Rightarrow F ]
\Rightarrow (B \Rightarrow \neg A)$](img95.png)
-
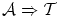
-
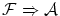
-
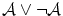
これらは「命題論理」の公理と呼ばれているものですが,もし,関係式が
や
のようなものを含んでいなければ,前述の「代数的な演算」の規則
に
を加えたもので,真理値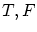 が決定でき,その関係式が恒真式かどうかが判ります。
が決定でき,その関係式が恒真式かどうかが判ります。
しかし,
のような関係式はこのような方法では真理値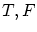 を決めることができません。
を決めることができません。
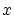 が動く範囲が
が動く範囲が
のように
有限ならばこの式は
と同じなので,真理値は上の「代数的な演算」の規則で決定できますが,一般には,
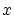 が動く範囲は無限個です。従って,別の方法に拠らなければなりません。
が動く範囲は無限個です。従って,別の方法に拠らなければなりません。
Yasunari SHIDAMA