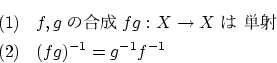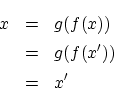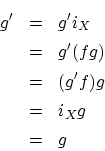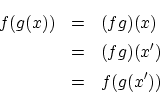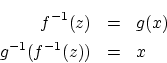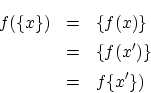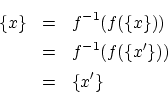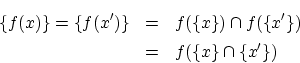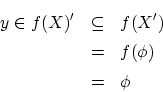


: この文書について...
: 単射,全射
: 逆写像
目次
 から
から への写像
への写像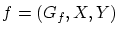 と
と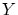 から
から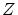 への写像
への写像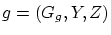 について
について
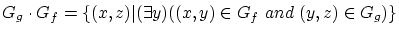 として
として
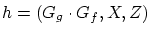 とおくと,
とおくと,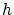 は
は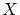 から
から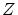 への写像です.これを
への写像です.これを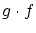 で表します.
で表します.
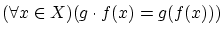 が成り立っています.
が成り立っています.
例
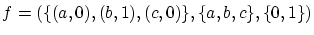
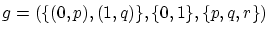
のとき
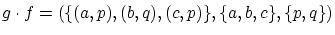
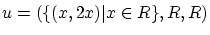
![$v=(\{ (y,\sin (y))\vert y\in R\} ,R,\left[ {-1,1} \right])$](img62.png)
のとき
![$g\cdot f=(\{ (x,\sin(2x))\vert x\in R\} ,R,\left[ {-1,1} \right])$](img63.png)
問題
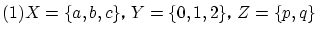 とします.このとき合成写像の列を作ってください.
とします.このとき合成写像の列を作ってください.
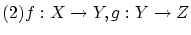 について以下を示して下さい.
について以下を示して下さい.
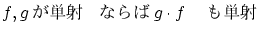
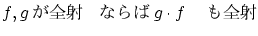
![$\left[ {恒等写像} \right]$](img68.png)
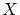 から
から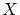 への全単射
への全単射 で
で
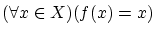 となるものを恒等写像と呼び
となるものを恒等写像と呼び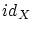 で表します.
で表します.
問題
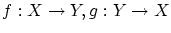 について以下を示して下さい.
について以下を示して下さい.
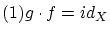 ならば
ならば は単射で
は単射で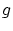 は全射
は全射
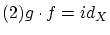 かつ
かつ
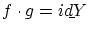 ならば
ならば は双射で
は双射で
以下の命題が成立っています。
- 命題3.3.1
-
のとき,写像の合成については結合律
が成り立つ。
- 証明
-
- 命題3.3.2
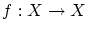 のとき
のとき
- 証明
-
- 命題3.3.3
 が
が
 であれば
であれば 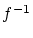 が存在して
が存在して
となります。
- 逆写像と証明
-
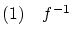 の存在性
これには,先ず
の存在性
これには,先ず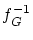 が関数のグラフになることを示せばよい。
が関数のグラフになることを示せばよい。
とおく。 が
が  だから
だから
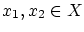 で
で
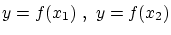 すなわち
すなわち
とすると
 が
が 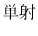 ですから
ですから
よって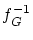 は関数のグラフになっています。。また,
は関数のグラフになっています。。また,
よって
で写像 X  X が定義できます。
X が定義できます。
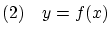 とおくと
とおくと
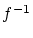 の定義より
の定義より
また
よって
- 命題3.3.4
-
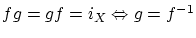
- 証明
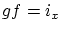 のとき
のとき
- 命題3.3.5
-
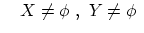 で
で
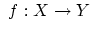 とするとき
とするとき
 が
が
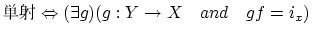
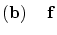 が
が
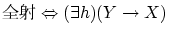
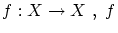 が
が
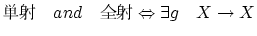
またこのような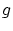 は一意に存在します。
は一意に存在します。
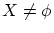
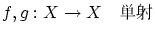 ならば
ならば
- 証明(a)
 が
が のとき
のとき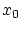 を
を のある元として
のある元として
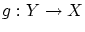 を以下のように定義します。
を以下のように定義します。
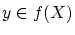 のとき
のとき
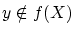 のとき
のとき
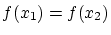 とすると
とすると が
が ですから
ですから
となり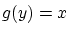 となる
となる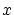 は唯一に定まる。
は唯一に定まる。
ここで、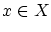 を任意にとると
を任意にとると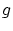 の定義から
の定義から
∴
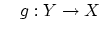 が存在して
が存在して
逆に、
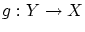 が存在して
が存在して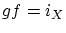 のとき
のとき
とすると
から
よって
- 証明(b)
 が
が とする。
とする。
 を以下のように定める。
を以下のように定める。
 について
について の元
の元 を一つ選び
を一つ選び
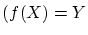 だから
だから
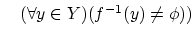
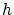 の定義から
の定義から
よって
よって
逆に
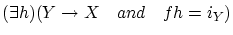 のとき
のとき
よって
よって

は

- 証明(c)
 が
が
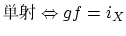
 が
が
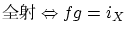
一意性は
とすると
よって
- 証明(d)
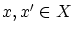 を任意にとり
を任意にとり
とすると
となり、 が
が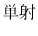 ですから
ですから
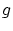 が
が ですから
ですから
よって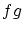 は
は
また任意の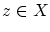 について
について
となる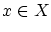 が存在する。これから
が存在する。これから
よって
よって
- 命題3.3.6
-
- (a)
とする。このとき
- (b)
- (c)
- (d)
- (e)
 が
が とする。このとき
とする。このとき
- 証明
- 定義より
です。
ここで、
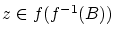 となる
となる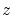 を任意に選ぶと
を任意に選ぶと
よって
よって任意の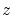 について
について
よって
 が
が のとき、
のとき、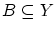 とする。
とする。 が
が ゆえ
ゆえ
よって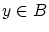 とすると
とすると
よって
よって
よって任意の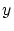 について
について
よって
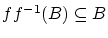 はすでに示したから
はすでに示したから
次に逆を言う。
とすると
よって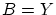 にとると
にとると
よって は
は
- 命題3.3.6(b)
- 証明
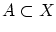 とする。
とする。
任意の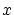 を選び
を選び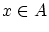 とすると
とすると
よって
よって任意の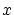 について
について
よって
よって
 が
が とする。
とする。
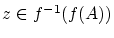 となる任意の
となる任意の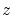 を選ぶと
を選ぶと
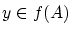 から
から
よって
 は
は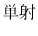 だから
だから
よって任意の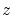 について
について
よって
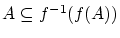 はすでに示したから
はすでに示したから
逆を言う
のとき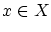 となる任意の
となる任意の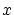 を選ぶと、
を選ぶと、
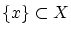 ゆえ
ゆえ
が成り立っている。
ここで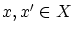 で
で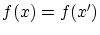 とすると
とすると
よって
よって
よって は
は
- 命題3.3.6(c)
- 証明
-
とする。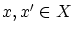 で
で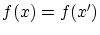 とすると
とすると
ここで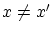 とすると
とすると
これは矛盾する。よって
よって は単射
は単射
逆に が
が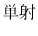 とすると
とすると
が成立するから
をいう。
とすると、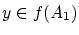 より
より
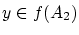 より
より
 は
は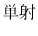 だから
だから
よって
よって
よって
- 命題3.3.6 (d)
- 証明
-
を仮定する。
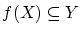 は成立しているから
は成立しているから
をいう。
ここで、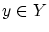 を任意に選び、
を任意に選び、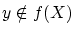 とすると
とすると
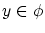 これは矛盾。よって
これは矛盾。よって
よって任意の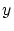 について
について
よって
逆に が
が のとき
のとき
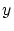 を任意に選び
を任意に選び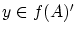 とする。
とする。
ここで
とすると
ですから
よって
これは が
が ですことに矛盾。ゆえに
ですことに矛盾。ゆえに
よって任意の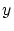 について
について
ゆえに
- 命題3.3.6(e)
 が
が とする。このとき
とする。このとき
- 証明
 が
が ゆえ
ゆえ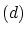 により
により
 が
が とすると
とすると
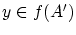 のとき
のとき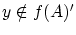 とすると
とすると
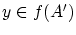 ですから
ですから
よって
これは矛盾。よって
逆に
のとき、任意の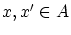 を選び
を選び
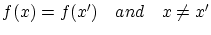 とすると
とすると
よって
これは矛盾。よって
よって は
は



: この文書について...
: 単射,全射
: 逆写像
目次
Yasunari SHIDAMA
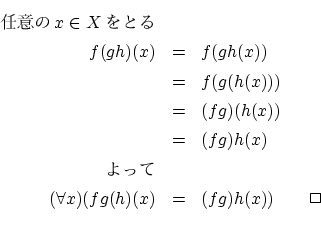
![]() のとき
のとき
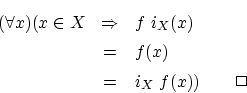
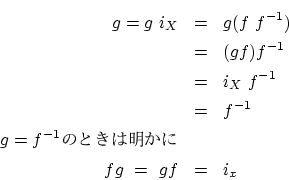
![]() が
が
![]()
![]()
![]() が
が
![]()
![]()
![]()
![]() ならば
ならば